典型例题分析
例3.1 已知单位反馈系统的开环传递函数为
试确定系统的稳定性或求系统稳时K的取值范围。
解 （1）系统(a)的K的稳定域
解法一（应用赫尔维茨判据） 由1+Ga (s)=0,可得系统(a)的特征方程为
应用赫尔维茨判据则可求得系统稳定的充要条件为
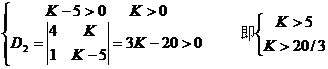
故K的稳定域为K＞20／3。
解法二（应用劳斯判据） 由特征方程可构造劳斯阵列如下：
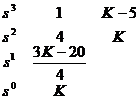
要使系统稳定，其第一列的元素必须全为正。同样也可以求得K的稳定域为K＞20／3。
(2)系统(b)的稳定性
解法一（应用赫尔维茨判据） 由1+Ga (s)=0,可得系统(b)的特征方程为
由于特征方程的系数全为正的，而
故可判断该闭环系统是不稳定的。
解法二（应用劳斯判据） 由特征方程可构造劳斯表如下：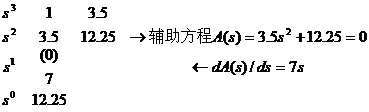
可见其第一列的元素不变号，故系统没有极点在右半开平面上。而由辅助方程
可解得系统有一对纯虚根p1，2=±j1.87。于是应用长除法由系统的特征方程
则可求得另一个系统极点为p3=-3.5。因此可判断该系统为临界稳定的。
讨论 由例题结果可见：（1）系统的开环稳定性和闭环稳定性是两回事，它们之间没有必然的联系。开环稳定的（如系统（b））其闭环未必稳定；开环不稳定的（如系统（a））其闭环不见得不稳定。所谓系统稳定性，指的是闭环的稳定性。从工程上着眼，为使系统易于控制和调试，通常希望系统的开环应是稳定的。（2）从判断系统的稳定性以及确定稳定裕度和参数的稳定域而言，赫尔维茨判据和劳斯判据是等效的。然而劳斯判据还可用来确定极点在左右两半平面上的分布情况，而且运算较为简便，故在实际中得到了较为广泛的应用。
例3.2 设单位反馈系统的开环传递函数为
试确定参数K和T稳定域。
解 由1+G(s)=0可得系统的特征方程为
于是可构造劳斯如下：
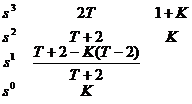
根据劳斯判据，要使系统稳定其劳斯表的第一列元素必须全为正的，即T＞0,
K＞0,T+2-K(T-2)＞0
故系统稳定时参数K和T的取值范围为
相应的K和T的稳定域，如图3.2所示。
例3.3 控制系统的结构图，如图A3.2所示。若系统以频率w=2rad/s持续振荡，试确定相应的参数K和 的值。
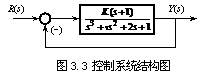解 由结构图可得系统的特征方程为
于是可构造劳斯表如下：
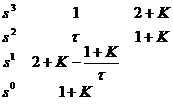
根据题意，闭环系统存在一对共轭纯虚根p1，2=±j2。这意味着劳斯表的 行全为零元素，即
。由辅助方程
解得一队共轭纯虚根
。
联立求解下列方程组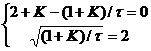
则可求得系统产生w=2rad/s的持续振荡时，参数K和
的取值为
例3.4 某液位控制系统的结构图，如图3.4(a)所示。图中hr为给定液面高度，h为实际液位，q1为进水流量，q2为用水流量。试判断系统的稳定性，并讨论使系统稳定的可能措施。
解 由结构图可得系统的特征方程为
式中K= KpKmK1K2为系统的开环增益。
分析上式可以看到：特征方程s1项，不满足各项系数均大于零的必要条件，故系统不稳定，而且无论如何调整系统参数Tm和K的大小均无法使系统稳定。这种并非参数设置不当而是由于系统结构所造成的不稳定系统，叫做结构性不稳定系统。要使这类系统稳定，必须改变原系统的结构。由3.7节可知，改善系统特性使闭环稳定有两种可行方案：
（1） 引入比例微分（PD）控制
在原系统的受控对象前引入PD控制器
，其结构图如图3.4(b)所示。由图可得，引入PD控制后系统的特征方程变成为
它已经不缺项，根据劳斯判据可求得系统稳定的充要条件为
。可见只要适当调整参数使
，便可确保闭环系统为稳定的。
（2） 引入局部负反馈回路
在受控系统或其部分环节的两端用局部负反馈回路包围它，以改善系统的特性使之稳定。现以图 A3.3(a)虚线所示的局部负反馈回路为例，说明如下。当伺服电动机两端用比例反馈回路包围后，其等效传递函数为
于是由1+Gk(s)=0可得结构改变后系统的特征方程为
它已经不缺项，应用劳斯判据可求得系统稳定的充要条件为K3＞TmKpK1K2。因此只要调整参数使条件成立，则可确保该闭环系统稳定。
例3.5 假设温度计放置在oC的恒温箱内，其传递函数为G(s)=1/(Ts+1)。现用温度计测量盛在容器内的水温，需要1分钟才能指示出实际水温的98%。试问：（1）该温度计的时间常数 T以及指示出实际水温的10%变化至90%所需的时间各为多少？（2）如果给容器加热，使水温以10oC/min的速度匀速上升，温度计的稳态指示误差有多大？
解 （1）
温度计的时间常数和系统暂态响应的上升时间为
或
当t=60s时y(t)=0.98。将此值代入上式，则可求得温度计的时间常数为
由
（2）温度计的稳态指示误差
温度计测温系统可视为等效的单位反馈系统，其结构图如图3.44所示。由闭环传递函数G(s)=1/(Ts+1)可知，a0 =b0=1。故系统为Ⅰ型，相应的Kv=K=1/T。而由题意可知r(t)=10t/60=t/6(oC
/s)，于是可求得温度计的稳态指示误差为
例3.6 设系统的结构图如图3.6所示，其中受控对象的传递函数为
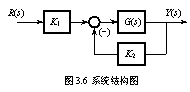
现拟采用负反馈的办法将调节时间减少到原来的1/10，而增益保持不变。试确定系统参数K1和K2的值。
解
根据题意，系统的期望闭环传递函数为
而由结构图可得，系统的实际闭环传递函数为
令F(t) =Fex(s),比较方程两边s的同幂次项系数，于是有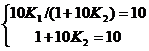
联立求解，则可求得系统参数的值为K1=10 K2=0.9。
例3.7 设控制系统的结构图如图3.7所示，其输入信号为单位斜坡函数（即r(t)=t）。要求：（1）当 和K1=1时，计算系统的暂态性能（超调量sp和调节时间ts）以及稳态误差；（2）若要求系统的单位阶跃响应的超调量sp=16.3%，峰值时间tp=1s，求参数K1和 的值，以及这时系统的跟踪稳态误差；（3）若要求超调量sp=16.3%和当输入信号以1.5度/秒匀速变化时跟踪稳态误差esr=0.1度，系统参数K1和的值应该如何调整？
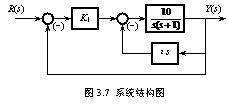
解 由结构图可知，系统的开、闭环传递函数为
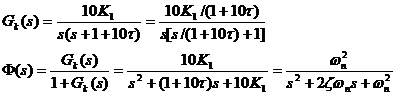
可见它是一个二阶规范系统，系统的开环增益为
。
（1）当K1=1和
（即局部反馈回路断开）时，由式(A3.9)可得这时系统的闭环传递函数为
式中
。于是由二阶系统性能指标表达式，则可求得系统的性能为
（2）当sp =16.3%和tp =1s时
由二阶规范系统的暂态性能指标表达式可得
而由式(A3.9)可得
故可求得系统的参数为
K1=1.316
=0.263
系统跟踪单位斜坡输入信号的稳态误差为
（3）当sp =16.3%和esr=0.1度时，由超调量sp =16.3% 可求得对应的阻尼比为
，根据题意r(t)=1.5t。于是由式(A3.9)和应用误差系数法可得
联立求解，则可得这时参数的值为
例3.8 位置随动系统的结构图如图3.8所示，已知系统的误差响应为
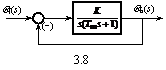e(t)=1.4e-1.07t -0.4e-3.73t
t≥0
(A3.10)试求：(1)系统参数K、Tm和特征参数 
的取值；（2）系统的暂态性能和稳态性能。
解 （1）系统参数和特征参数的取值
由结构图3.27可得，位置随动系统的开、闭环传递函数为
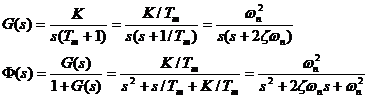
可见该系统为Ⅰ型的，则Kp=∞， Kv=K, Ka=0。由式(A3.10)可得：系统的跟踪稳态误差
，于是可以推断其输入信号为阶跃函数；闭环极点为p1=-1.07,
p2=-3.73。则可求得系统的特征多项式为
于是有
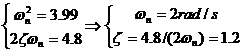
故系统的参数为
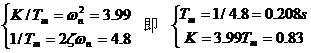
(2)系统的暂态性能和稳态性能
系统工作在过阻尼状态，其暂态响应为非周期的。于是可求得系统的暂态
性能为
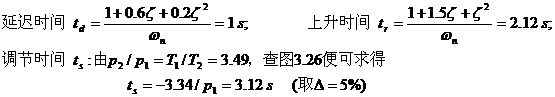系统的稳态性能：跟踪阶跃输入信号无稳态误差；跟踪单位斜坡输入信号的稳态误差为
esr= 1/Kv = 1/K = 1/0.83 = 1.2（度）
说明 3.5节已经指出：一阶和二阶系统的暂态性能与其特征参数
相对应，而特征参数又与系统传递函数的规范形式相联系。例3.5-3.8正是利用低阶系统传递函数的规范形式和特征参数与暂态性能之间的内在联系来求解的。这也是低阶系统和具有主导极点的高阶系统解题的基本思路。
例3.9 已知控制系统的结构图如图A3.8所示，图中G1(s)环节的单位阶跃响应为8(1-
e-5t)/5。试问：（1）若r(t)=20×1(t) 和d(t)=0 时，系统响应的超调量、调节时间以及输出的稳态值各为多大？（2）若r(t)=20×1(t) 和d(t)=1(t) 时，系统的稳态误差为何值？
解 （1）当r(t) =20×1(t) 和d(t)=0 时系统的时间响应特性
根据题意可知：
于是由系统的结构图可得，闭环传递函数为
其中G2(s)=2/(s+4)为局部反馈回路的等效传递函数。
应用终值定理可求得，在r(t)=20×1(t)作用下系统输出的稳态值为
由系统的特征多项式
故可求得系统的暂态性能为
（2）当r(t)=20×1(t) 和d(t)=1(t) 时系统的稳态误差
由结构图可知：系统的误差是按折算至输入端定义的：系统的开环传递函数为
可见该系统为0型的，其开环增益K=4。于是系统的跟踪稳态误差为
由结构图可得，按折算至输入端定义时系统的扰动误差传递函数为
应用终值定理，可求得系统的扰动稳态误差为
考虑到在实际系统中扰动信号的作用方向可能改变，通常取系统的稳态误差为跟踪稳态误差与扰动稳态误差的绝对值之和。故可得系统的稳态误差为
ess=∣esr∣+∣esd∣=4+0.5=4.5
讨论 系统扰动误差的定义方法有两种，按折算至输入端和按折算至输出端来定义。相应的系统扰动误差传递函数的表达式也有两种：按折算至输出端考虑，其表达式如(3.141)所示；按折算至输入端考虑，其表达式如(2.73)所示。
两种定义方法和相应的Fed(s)的两种表达式都是用来描述系统的扰动误差，因而它们的分析方法和基本结论是一致的。但由于定义的方法不同和Fed(s)表达式不一样，它们的具体结论也将有所差别。如果系统的扰动稳态误差为一有限值（包括0），则按折算至输入端定义时，由
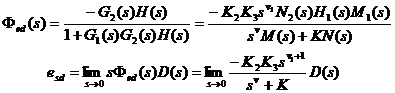
分析上述两式可以看到：对于多项式扰动信号
当多项式扰动信号的次数k＜v1时，则esd=0；当k=v1时，则esd为一有限值，且v=0时则esd= -K2K3D1
/（1+ K1K2K3）≈-D1 / K1 ，v1≥1时 esd = -D1 / K1 ；当k＞v1 时则系统的扰动误差将随着时间的推移而不断变大，当t→∞时其扰动终值误差将趋于无穷大。由此可见，按折算至输入端定义时所得的结论，与