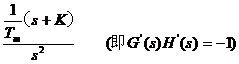例4.1 根轨迹的分支数:等于开环传递函数的极点数。如:
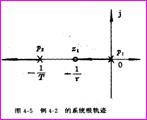
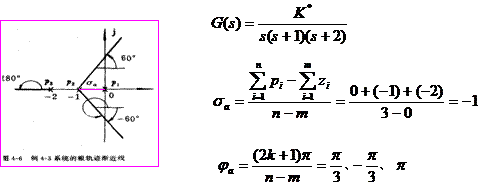 例4.2
根轨迹的渐近线。如已知单位反馈系统的开环传递函数为
例4.2
根轨迹的渐近线。如已知单位反馈系统的开环传递函数为
![]()
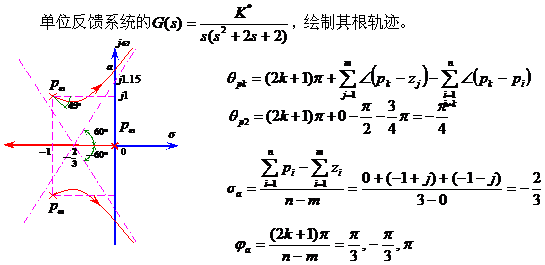 例4.3
例4.3
![]()
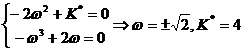
![]()
![]()
例4. 4 某单位反馈系统传递函数为

![]() 开环增益为 K=K*/2 ,K的稳定域为 0<K<3 .
开环增益为 K=K*/2 ,K的稳定域为 0<K<3 .
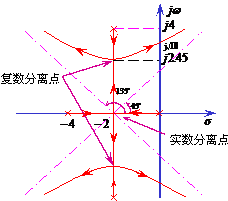
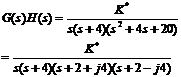 例4.5
例4.5
![]() 例4.6
例4.6
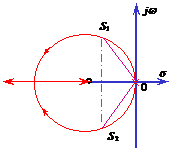
![]()
![]()
![]() 例4.7
例4.7
解 原系统的闭环特征方程为
D(s)=1+G(s)H(s)=s(5s+1)+5(Tas+1)=0
将和参数有关的各项归并在一起,上式可写为
![]() 5s2+s+5+5Tas=0
5s2+s+5+5Tas=0
所以
就是新的开环传函,而5 相当于新的开环增益。
解题关键:要将开环传函变形,将非开环增益的参数变换到开环增益的地位。
例4.8 求Tm从0 → ∞时的根轨迹
原系统的闭环特征方程为
Tms2
+ s + K = 0

即 s2
+ s/Tm + K/Tm
= 0
得新的特征方程为
s2
+ (s+ K)/ Tm = 0
则新的等效开环传函为