例8.1 e(t)=e^at,试写出e^*(t)表达式。

解：

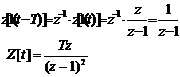例8.2 已知e(t)=1(t-T),求Z变换E(z)。

解：

例8.3 已知e(t)=t ×e^-at,求Z变换E(z)。

解：已知单位斜坡信号的z变换为

根据复数位移定理，有

例8.4 试求bⁿcoswt的Z变换。

解：由变换表

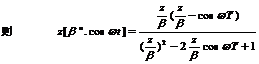
例8.5 已知z变换函数，E(z)=，试求其z反变换。

解：首先将E(z)/z展开成部分分式

所以e(nT)=(-1+2ⁿ)×10

e^*(t)=e(0)d(t)+e(T)d(t-T)+e(2T)d(t-2T)+…

=0+10d(t-T)+30d(t-2T)+ 70d(t-3T)+…

例8.6 已知z变换函数 ，试求其z反变换。

解：因为

查表得 e(t)=1(t)-e^-at 则 e(nT)=1-e^-anT

所以 e*(t)=e(0)d(t)+e(T)d(t-T)+e(2T)d(t-2T)+…

=0+(1-e^-aT)d(t-T)+(1-e^-2aT)d(t-2T)+(1-e^-3aT)d(t-3T)+…

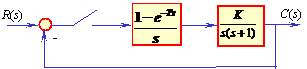例8.7 设系统的结构图如下图所示，采样周期T=1s 。设 K=10,试分析系统的稳定性，并求系统的临界放大系数。

解： ⑴ 由图得

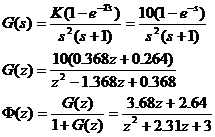
由此得系统特征方程为

z²+2.31z+3=0

求解得一对共轭复根

l₁=-1.156＋j1.29， l₂=-1.156-j1.29

分布在单位圆外，因此系统是不稳定的。

⑵ 由系统开环脉冲传递函数

求得系统特征方程为

z²-(1.368-0.368K)z+(0.368+0.264K)=0

进行w变换得

(2.736-0.104K)w²+(1.264-0.528K)w+0.632K=0

列劳氏表计算

w² 2.736-0.104K 0.632K

w¹ 1.264-0.528K 0

w⁰ 0.632K

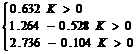为使系统稳定，须有

得到系统的临界放大系数为：K_c=2.4

例8.8 设系统的结构图如下图所示，K=1, T=0.1s ,r(t)=1(t)+t, 求系统的稳态误差。

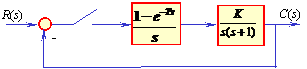
解：系统的开环传递函数为

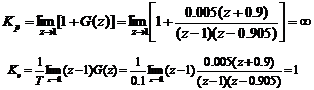把T=0.1代入化简得

系统的稳态误差为