第一套
一、单项选择填空(每小题4分,共20分)
1. 统不稳定时,其稳定误差为( )
1)+∞ 2)-∞ 3)0 4)以上都不对
2. 2-1-2型渐近对数幅频特性描述的闭环系统一定( )
1)稳定 2)不稳定 3)条件稳定 4)说不清
3. 由纯积分环节经单位反馈而形成的闭环系统超调量为( )
1)0 2)16.3% 3)无超量 4)以上都对
4. 描述函数描述了( )系统的性能。
1)非线性系统 2)本质非线性系统 3)线性、非线性系统 4)以上都错
5. 采样周期为( )的系统是连续系统。
1)0 2)∞ 3)需经严格证明 4)以上都错
二、简化结构图求传递函数C(s)/R(s)
(每小题8分,共16分)
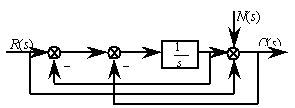
1.
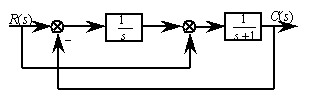 2.
2.
三、单位负反馈系统的零初始条件下的单位阶跃响应为 (每小题5分,共20分)
![]()
1. 析开环、闭环稳定性;
2. 超调量;
3. 求Δ=±0.02L(¥)时,调节时间;
4. 求阶跃响应时的稳态误差。
四、单位负反馈系统的开环传递函数为 (每小题8分,共16分)
![]()
1. 绘制开环根轨迹图;
2. 决定闭环稳定的k1的范围。
![]() 五、单位负反馈系统开环传递函数为 (每小题8分,共16分)
五、单位负反馈系统开环传递函数为 (每小题8分,共16分)
1. 绘制开环伯德图;
2. 分析闭环稳定性。
![]() 六、采样周期为1s、带零阶保持的误差采样系统,连续部分的传递函数为 (12分)
六、采样周期为1s、带零阶保持的误差采样系统,连续部分的传递函数为 (12分)
1. 分析开、闭环稳定性;
2. 若闭环稳定,则求单位阶跃输入下的稳定误差。
![]() 一、单项选择填空 (每小题4分,共20分)
一、单项选择填空 (每小题4分,共20分)
1. 在1-2-3渐近对数幅频特性图上,开环传递函数为
...的闭环系统是( )的。
1 ) 稳定 2 ) 绝对不稳定 3
) 临界稳定 ......4 ) 以上都错
2. 采样开关使系统闭环稳定性变( )
![]()
![]() 1)好 2)坏 3)说不清 4)以上都对
1)好 2)坏 3)说不清 4)以上都对
3. 传递函数
..的状态变量表达式( )为
1 ) 仅 2 )不仅 3
)仅为但不能观测 .........4) 不仅为且能控
4. 配置线性系统极点的( )条件是该系统完全能控。
1)充分 2)必要 3)充分必要 4)既不充分也不必要
5. 奈奎斯特图( )能描述系统的稳定性。
1)仅 2)仅开环系统 3)仅闭环系统 4)以上都错
二、简化结构图求传递函数G(s)/R(s) (每小题8分 共16分)
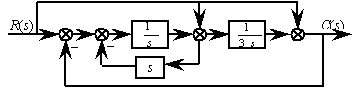 1.
1.
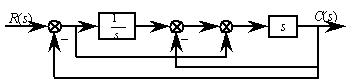
2.
三、控制系统的开环特征方程为S3+S3+S=0,试组织任-单位负反馈闭环系统:(每小题10分,共20分)
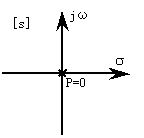 1. 绘制闭环系统结构图;
1. 绘制闭环系统结构图;
2. 分析闭环系统的稳定性。
四、系统的开环根轨迹如图所示 (每小题5分,共15分)
1. 要求系统闭环极点为S1,2 =-1±j1;
2. 应该在误差通道至少增加什么环节,绘制相应结构图;
3. 求这时系统的相应开环传递函数。
![]() 五、单位负反馈系统的开环传递函数为 (每小题5分,共20分)
五、单位负反馈系统的开环传递函数为 (每小题5分,共20分)
1. 绘制开环伯德图且分析闭环稳定性;
2. 要使系统开环有2-1-3型渐近对数且闭环特征的系统,应加入何种最简单的校正装置;
1)写出校正装置的传递函数;
2)绘制校正后的系统开环伯德图。
六、系统方框图如图所示:(每小题3分,共9分)
1. 写出系统可能的描述函数;
2. 系统是否存在稳定的自振荡?为什么?
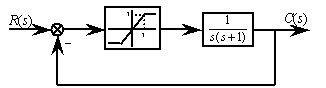 3. 是否存在稳定自振点?若存在,求出来。
3. 是否存在稳定自振点?若存在,求出来。
第三套
一、改错或判断正确性(每小题4分,共20分)
1. 一切闭环稳定系统总有稳态性能。
2. 只有带保持器的离散系统才需满足采样定理。
3. 稳定误差为∞的系统均不稳定。
4. 在开环伯德图上判别闭环稳定性比采用奈魁斯特判据更简单方便。
5. 能控性状态变量表达式的状态均不可测量。
二、举一个任意例子(每小题5分,共20分)
![]() 1. 若其传递函数为:
1. 若其传递函数为:
2. 绘制该系统的原理示意图;
3. 绘制该系统的结构图;
 4. 简化相应结构图校验其传递函数。
4. 简化相应结构图校验其传递函数。
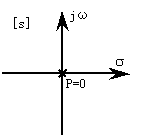
三、系统的开环根轨迹如图所示(每小题5分,共15分)
1. 采用串联校正
1)使系统的根轨迹出现一个圆而开、闭环稳定性不变;
2)闭环极点过S1.2= -1±j;
2. 求校正装置的传递函数;
3. 绘制校正后系统的根轨迹图。
![]() 四、负反馈系统的开环传递函数为(每小题5分,共15分)
四、负反馈系统的开环传递函数为(每小题5分,共15分)
1. 绘制开环极坐标圆;
2. 用奈魁斯特判据分析闭环稳定性;
3. 确定单位斜坡输入时的稳态误差。
五、线性单位负反馈系统方框图如图:(每小题2.5分,共10分)
1.  求应有的描述函数;
求应有的描述函数;
2. 分析闭环稳定性;
3. 系统是否存在稳定的自振荡?为什么?
4. 若存在,求相应稳定参数。
![]() 六、系统传递函数为:(每小题5分,共20分)
六、系统传递函数为:(每小题5分,共20分)
1. 做出能直接而显然的配置极点的实现;
2. 把闭环极点配置在 Sg1.2=–2±j2处;
1)求状态反馈阵K;
2)求状态反馈前后的状态变量表达式;
3)求状态反馈前后的系统的结构图。
第四套
一、填空 (每小题4分,共20分)
1. 典型一阶系统的T=20,k=80,则超调量为( );当△=0.02L(¥)时,调节时间为( )S。
2. 2-1-2型渐近对数幅频特性描述的系统具有常值误差的( )条件是( )。
3. 系统存在任意极点时的观测器的( )条件是( )。
4. 与连续系统相比,非线性的特点是( )、( )、( )和( )。
5. 对控制系统的要求是( )、( )、( )和 ( )。
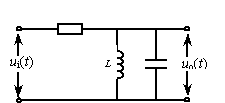 二、求如图系统的递函数U0(s)/Ui(s)。(13分)
二、求如图系统的递函数U0(s)/Ui(s)。(13分)
三、求超调量为16.3%,△=0.02L(¥)时的典型二阶系统的微分方程和传递函数
(13分).
四、系统开环根轨迹的一部分为以(0,j0)为圆点、半径为2的圆。 (每小题6分,共18分)
1. 求开环传递函数;
2. 绘制系统结构图;
3. 用劳斯判据分析开、闭环稳定性。
五、系统的闭环特征方程为 (每小题6分,共18分)
S3+3S2+2S+1=0
1. 绘制一种二环极坐标图;
2. 用奈魁斯特判据分析闭环稳定性;
3. 这些情况下,求任一种参考输入信号,使系统稳态误差为2%。
六、![]() 误差采用周期为1s的采样系统,连续部分的开环传递函数为:(每小题6分,共18分)
误差采用周期为1s的采样系统,连续部分的开环传递函数为:(每小题6分,共18分)
1. 绘制开环根轨迹图;
2. 决定闭环稳定性;
3. 求单位阶跃输入时的稳态误差系数和稳态误差。
第五套
一、填空(每小题4分,共20分)
1. 频率特性是( )。
2. 奈魁斯特判据是从( )判断闭环系统的( )。
3. 线性系统和线性化系统同样都视为( )。
4. 正、负反馈系统的根轨迹在绘制时有( )不同。
5. 就稳态误差而言线性连续系统和线性采样系统均可用( )计算。
二、简答:(每小题 5分,共15 分)
1. 叙述微分方程和传递函数的关系及相应条件;
2. 传递函数为G(s)=C(s) / R(s) =(2S+5) / S3 的微分方程是什么?
3. 零初始条件下,单位脉冲响应h(t)=1-e –TS的微分方程是什么?为什么?
三、某系统的闭环传递函数为:(每小题 5分,共15 分)
![]()
1. 求超调量或足够精确的近似值;
2. 求单位阶跃响应下的稳态误差;
3. 该闭环系统稳定吗?为什么?
![]() 四、单位负反馈系统的开环传递函数为:(每小题5 分,共 15分)
四、单位负反馈系统的开环传递函数为:(每小题5 分,共 15分)
1. 求相角裕量γ= 45º 的K值;
2. 计算单位斜坡信号作用时,系统稳态误差为1%的K值;
3. 要使系统开环根轨迹既含有一个圆且圆周过各开环极点中点,求这时的开环传递函数。
五、2-1-2型渐近对数幅频特性的对数幅值穿越频率为ωc=10S-1且两端有界的频段为100频程,求
(每小题5 分,共 15分)
1. 开环传递函数G(s);
2. 相角裕量γ;
3. 稳态误差系数。
六、线性系统的状态变量表达式为 (每小题 5分,共 20分)
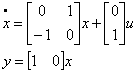
1. 状态观测器是否存在?为什么?
2. 如果存在,把观测器极点配置在-1±j,求观测器的运动方程及相应的运动参数;
3. 写出含状态观测器系统的状态变量表达式;
4. 绘制观测器,设计前后系统的结构图。
|
Copyright 2007-2008 西南科技大学网络教育学院. All Rights Reserved |