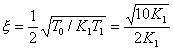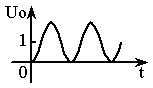实验二 典型系统瞬态响应和稳定性
1.典型二阶系统
①典型二阶系统的方块图及传函
图2-1图是典型二阶系统原理方块图，其中T0=1S，T1=0.1S,K1分别为10、5、2.5、1。
开环传函：其中
=开环增益
闭环传涵：
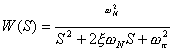，其中
|
各参数 |
|
|
|
|||
|
K |
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
1 |
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
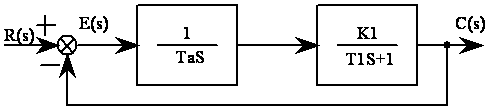
图2-1
②模拟电路图：见图2-2
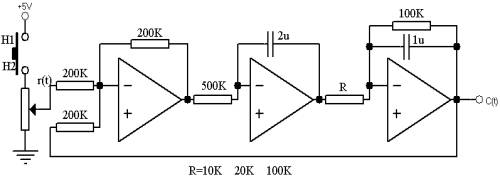
图2-2
2.典型三阶系统
①典型三阶系统的方块图：见图2-3
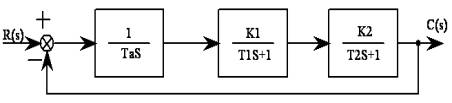
图2-3
开环传递函数为：
其中，
（开环增益）
②模拟电路图：见图2-4
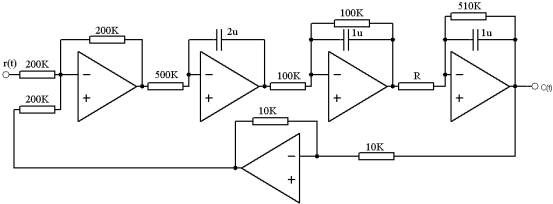
图2-4
开环传函为
（其中
）
系统的特征方程为
，
由Routh判据，得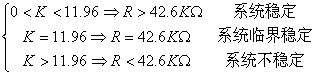
3.实验内容及步骤
准备：将“信号源单元”（U1 SG）的ST插针和+5V插针用“短路块”短接，使运算放大器反馈网络上的场效应管3DJ6夹断。
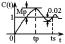
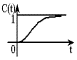
（1）典型二阶系统瞬态性能指标的测试。
①按图2-2接线，R=10K。
②用示波器观察系统阶跃响应C（t），测量并记录超调量
，峰值时间
和调节时间
。记录表2中。
③分别按R=20K；40K；100K改变系统开环增益，观察相应的阶跃响应C（t），测量并记录性能指标
、
和
，及系统的稳定性，并将测量值和计算值（实验前必须按公式计算出）比较。参数取值及响应曲线，详见表2。
表2
|
参数 |
R (KΩ) |
K (1/S) |
Wn (1/S) |
ξ |
C(tp) |
C(∞) |
MP(%) |
Tp(S) |
Ts(S) |
阶跃响应曲线 |
|
|
测量值 计算值 |
测量值 计算值 |
测量值 计算值 |
|||||||||
|
0<ξ<1 欠阻尼阶跃响应为衰减振荡 |
10 |
10 |
10 |
|
1.2 |
1 |
20 25 |
0.4 0.36 |
0.75 0.8 |
1 |
|
|
20 |
5 |
|
|
1.18 |
1 |
18 20 |
0.2 0.3 |
0.8 0.8 |
0 |
||
|
ξ=1临界阻尼阶跃响应为衰减振荡 |
40 |
2.5 |
5 |
1 |
------ |
1 |
------- |
------- |
1.2 1.15 |
1 |
|
|
0 |
|||||||||||
|
ξ>1过阻尼响应为单调指数曲线 |
100 |
1 |
|
|
------ |
1 |
------- |
------- |
15 15.6 |
1 |
|
|
0 |
|||||||||||
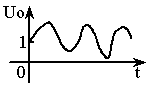
（2）典型三阶系统的性能
①按图2-4接线，R=30K。
②观察系统的阶跃响应，并记录波形。
③减小开环增益（R=42。6K；100K），观察系统的阶跃响应。参数取值及响应曲线详见表3。
表3
|
|
K |
输出波形 |
稳定性 |
|
30 |
17 |
|
不稳定（发散） |
|
42.6 |
11.96 |
|
临界稳定（等幅振荡） |
|
100 |
5.1 |
|
稳定（衰减振荡） |
