实验六 非线性系统
1.实验的原理方块图及模拟电路图简介
相平面图表征系统在各种初始条件下的运动过程，相轨迹则表征系统在某个初始条件下的运动过程，相轨迹可用图解法求得，也可用实验法直接获得。当改变阶跃信号的幅值，即改变系统的初始条件时，便获得-系列相轨迹。根据相轨迹的形状和位置就能分析系统的瞬态响应和稳态误差。
（1）继电型非线性系统原理方块图如图6-1所示，图6-2是它的模拟电路图
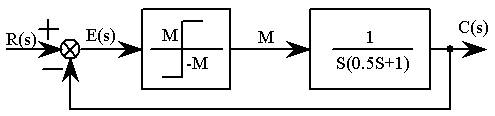
图6-1
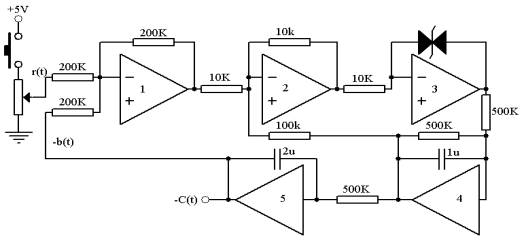
图6-2 继电型非线性系统模拟电路
图6-1 所示非线性系统用下述方法表示
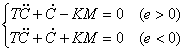（6-1）
式中T为时间常数
，K为线性部分开环增益
，M为稳压管稳压值。采用
和
为相平面座标，以及考虑
，
（6-2）
，
（6-3）
则式（6-1）变为
（6-4）
代入
、
以及所选用稳压值M，应用等倾线法作出当初始条件为
时的相轨迹，改变
值就可以得到一簇相轨迹。
图6-1 所示系统的相轨迹曲线如图6-3所示。
图6-3 图6-1 所示系统相轨迹
图6-3中的纵坐标轴将相平面分成两个区域，（Ⅰ和Ⅱ）e轴是两组相轨迹的分界线，系统在阶跃信号下，在区域Ⅰ内，例如在初始点A开始沿相轨迹运动到分界线上的点B，从B点开始在区域Ⅱ内，沿区域Ⅱ内的相轨迹运动到点C再进入区域Ⅰ，经过几次往返运动，若是理想继电特性，则系统逐渐收敛于原点。
（2）带速度负反馈的继电型非线性系统原理方块图如图6-4所示。图6-2中的虚线用导线连接，则图6-2就是图6-4的模拟电路。
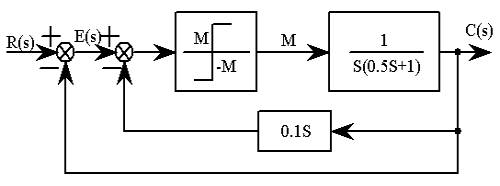
图6-4
带速度负反馈续电型非线性系统
相轨迹示于图6-5。显然，继电型非线性系统采用速度反馈可以减少超调量
。缩短调节时间
，减小振荡次数。
图中分界线由方程
（6-5）
确定，式中
为反馈系数（图6-4中，
）。
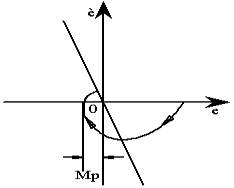
图6-5
图6-4的相轨迹
（3）饱和非线性系统原理方块图如图6-6所示。
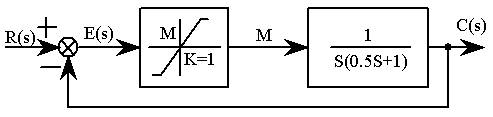
图6—6 饱和非线性系统
图6——7是它的模拟电路图
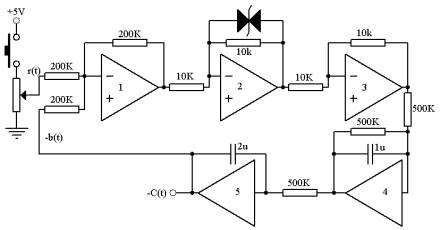
图6—7 饱和非线性系统模拟电路
图6——6所示系统由下述方程表示：
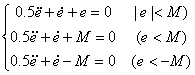
因此，直线e=M和e=-M将相平面（e-e）分成三个区域，如图6—8所示，
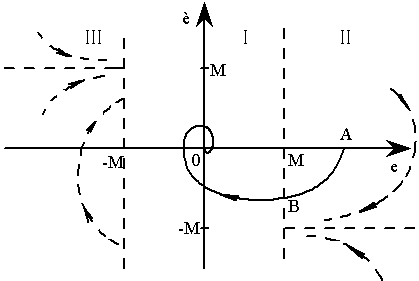
图6——8，图6——6所示系统的相轨迹
假设初始点为A,则从点A开始沿区域Ⅱ的相轨迹运动至分界线上的点B进入区域Ⅰ，再从点B开始沿区域Ⅰ的相轨迹运动，最后收敛于稳定焦点（原点）。
从图6-2和图6-7中可看出，1#运算放大器的输出是（-e），而4#运算放大器的输出为（-e），而4#运算放大器的输出
（即
）因此将1#运算放大器的输出接至示波器的X轴输入端，而将4#运算放大器的输出接至示波器的Y轴输入端，这样在示波器屏上就可获得
相平面上的相轨迹曲线。
2.实验内容及步骤
准备：将信号源单元（
）的ST的插针和+5V插针用“短路块”短接。
实验步骤：
（1）用相轨迹分析继电型非线性系统在阶跃信号下的瞬态响应和稳态误差。
①按图6-2接线
②在系统输入端分别施加及撤去幅值为5V、4V、3V、2V和1V电压时，用示波器观察并记录系统
平面上的相轨迹。测量在5V阶跃信号下系统的超调量
及振荡次数。
（2）用相轨迹分析带速度负反馈继电器型线性系统在阶跃信号下的瞬态响应和稳压误差。
①将图6-2中的虚线用导线连接好
②在系统输入端加入阶跃信号（5V、4V、3V、2V和1V），用示波器观察并记录系统在
平面的相轨迹，测量在5V阶跃信号下系统的超调量及扬荡次数。
（3）用相轨迹分析饱和非线性系统在阶跃信号下的瞬态响应和稳态误差。
①按图6-7接线；
②用（1）②。
3.实验结果分析
（1）研究带速度负反馈继电型非线性系统动态性能。
实验测得数据如表6-1所示
表6-1 （当
时）
|
|
不带速度负反馈的继电型非线性系统 |
带速度负反馈的继电型非线性系统 |
|
|
0.2V |
0.05V |
|
振荡次数 |
2次 |
无 |
很显然，当继电型非线性系统加上速度负反馈可以减少超调量，即平稳性加大，缩短调节时间
，减小振荡次数，系统的快速性得到提高。
（2）研究饱和非线性系统
通过实验，测得此时当
阶跃输入时，系统的超调为0.4V，且无振荡。
由于饱和特性在大信号时的等效增益很低，故带饱和非线性的控制系统，一般在大起始偏离下总具有收敛的性质，系统最终可能稳定，最坏的情况是自振，而不会造成愈大的不稳定状态。当然，如果饱和点过低，则在提高系统平稳性的同时，将使系统的快速性和稳态跟踪精度有所下降。
（3）三种非线性系统的相轨迹图，如图6-9所示。
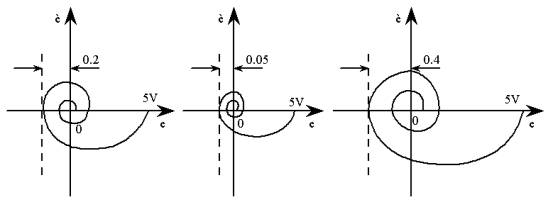
不带速度负饭的继电型系统 带速度负饭的继电型系统 饱和非线性系统