第二章 自控系统的数学模型

本章讲述的内容很多,牵扯到数学和物理系统的一些理论知识,有些需要进一步回顾,有些需要加深理解，特别是对时间域和复频率域的多种数学描述方法，各种模型之间的对应转换关系，都比较复杂。学习和复习好这些基础知识，对下一步深入讨论自动控制的具体方法至关重要。

1. 基本要求

（1）确理解数字模型的特点，对系统的相似性、简化性、动态模型、静态模型、输入变量、输出变量、中间变量等概念，要准确掌握。

（2）了解动态微分方程建立的一般方法及小偏差线性化的方法。

（3）掌握运用拉氏变换解微分方程的方法，并对解的结构、运动模态与特征根的关系、零输入响应、零状态响应等概念，有清楚的理解。

（4）会用MATLAB方法进行部分方式展开。对低阶的微分方程，能用部分分式展开法或留数法公式进行简单计算。

（5）正确理传递函数的定义、性质和意义，特别对传递函数微观结构的分析要准确掌握。

（6）正确理解由传递函数派生出来的系统的开环传递函数，闭环传递函数，前向传递函数的定义，并对重要传递函数如：控制输入下闭环传递函数，扰动输入下闭环传递数函数，误差传递函数，典型环节传递函数，能够熟练掌握。

（7）掌握系统结构图和信号流图两种数学图形的定义和组成方法，熟练地掌握等效变换代数法则，简化图形结构，并能用梅逊公式求系统传递函数。

（8）正确理解两种数学模型之间的对应关系，两种数学图型之间对应关系，以及模型和图形之间的对应关系，利用以上知识，熟练地将它们进行相互转换。

2. 内容提要及小结

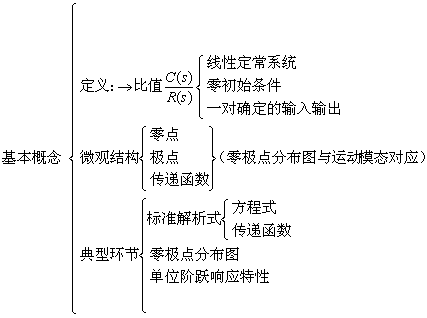
本章主要介绍数学模型的建立方法，作为线性系统数学模型的形式，介绍了两种解析式和两种图解法，对于每一种型式的基本概念，基本建立方法及运算，用以下提要方式表示出来。

（1）微分方程式

(2) 传递函数

（3）结构图

注意几点：

1. 相加点与分支点相邻，一般不能随便交换。

2、

3. 直接应用梅逊公式时，负反馈符号要记入反馈通路中的方框中去。另外对于互不接触回路的区分，特别要注意相加点与分支点相邻处的情况。

4. 结构图可同时表示多个输入与输出的关系，这比其它几种解析式模型方便的多，并可由图直接写出任意个输入下总响应。如：运用叠加原理，当给定输入和扰动输入同时作用时，则有C(s)＝G_r(s)R(s)＋G_d(s)D(s)

（4）信号流图

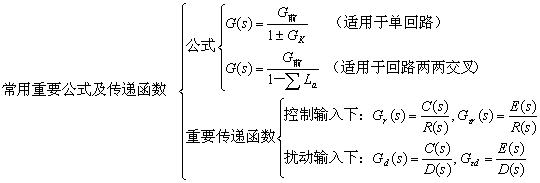
重要公式→梅逊公式 梅逊公式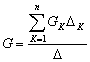

注意两点：

1、搞清公式中各部分含义；

2、公式只能用于等输入节点与较出节点之间的传播，不能等不含输入节点情况下，任意两混合节点之间的传较。

四种模型之间的转换关系可用图2－1表示

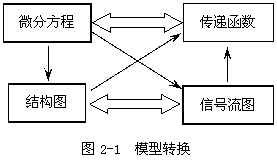
考核知识点：建立描述控制系统运动的微分方程；控制系统的传递函数、方框图及其简化、信号流图及梅森公式等。

重点：传递函数定义、建立控制系统的传递函数。

难点：从系统原理图建立拉氏变换方程组。