第四章 自控系统的根轨迹分析

1．基本要求

通过本章学习，应当做到：

（1）掌握开环根轨迹增益K^*(或K_g)（或开环比例系数K）变化时系统闭环根轨迹的绘制方法。理解和熟记根轨迹的绘制法则，尤其是实轴上根轨迹的确定、分离点及渐近线的计算方法、根轨迹与虚轴的交点坐标及出射角和入射角的确定。会利用幅值方程求特定的K值。

（2）了解闭环零、极点的分布和系统阶跃响应的定性关系及系统根轨迹分析的基本思路。正确理解偶极子和主导极点等基本概念，会用主导极点的概念估算系统的性能指标。

（3）了解0°根轨迹、参变量根轨迹及非最小相位根轨迹绘制的基本思路。

2．内容提要

本章主要介绍了根轨迹的基本概念、控制系统根轨迹的绘制方法以及根轨迹法在控制系统分析中的应用。

（1）根轨迹的基本概念

根轨迹是当系统中某参数（如开环根轨迹增益K_g）由0～∞变化时，系统的闭环极点在s平面上移动的轨迹。求出不同K_g值时的闭环极点，在s平面上逐点绘制即可得到系统的闭环根轨迹。但人工绘制即笨又繁，很不实用。根轨迹法的基本思路是：在已知开环零、极点分布的基础上，依据根轨迹法则，确定闭环零、极点的分布。再利用主导极点的概念，对系统的阶跃响应进行定性分析和定量估算。

（2）根轨迹方程

根轨迹方程实质上是系统闭环特征方程的变形。负反馈系统根轨迹方程的一般形式为

根轨迹方程的幅值平衡条件和幅角平衡条件分别称之为根轨迹的幅值方程和幅角方程。系统根轨迹方程的幅值方程和幅角方程由如下二式给出：

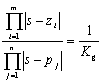
幅角方程是决定根轨迹的充分必要条件。系统的根轨迹可依据其幅角方程绘制，幅值方程主要用来确定根轨迹上各点对应的增益值。

（3） 绘制系统轨迹的基本法则

根据系统的根轨迹方程式，按照绘制系统根轨迹的基本法则，即可由系统开环零极点的分布直接绘制出闭环系统的概略根轨迹。教材上给出了当系统的开环根轨迹增益K_g由0～∞变化时，绘制系统180°根轨迹的基本法则。

（4）控制系统的根轨迹分析

控制系统的根轨迹分析即应用闭环系统的根轨迹图，分析系统的稳定性、计算系统的动态性能和稳态性能，或在根轨迹图上可以进行反馈系统的综合或校正。

当系统的根轨迹段位于左半s平面时，系统稳定。否则，系统必然存在不稳定的闭环根。当系统为条件稳定时，根轨迹与s平面的交点即其临界稳定条件。

利用根轨迹得到闭环零、极点在s平面的分布情况，可以写出系统的闭环传递函数，进行系统动态性能的分析。系统的闭环零点由系统的开环传递函数直接给出，系统的闭环极点需应用根轨迹图试探确定。如果系统满足闭环主导极点的分布规律，可以应用闭环主导极点的概念把高阶系统简化为低阶系统，对高阶系统的性能近似估算。

（5）附加开环零极点对根轨迹的影响

根轨迹是根据开环零极点的分布绘制的，系统开环零极点的分布影响着根轨迹的形状。通过附加开环零极点，可以改造系统根轨迹的形状，使系统具有满意的性能指标。增加一个开环实零点，将使系统的根轨迹向左偏移，提高了系统的稳定度，并有利于改善系统的动态性能。开环负实零点离虚轴越近，这种作用越大。增加一个开环实极点，将使系统的根轨迹向右偏移，降低了系统的稳定度，有损于系统的动态性能，使得系统响应的快速性变差。开环负实极点离虚轴越近，这种作用越大。开环零点和极点重合或相近时，二者构成开环偶极子。合理配置偶极子中的开环零极点，可以在不影响动态性能的基础上，改善系统的稳态形能。

考核知识点：控制系统的根轨迹、根轨迹方程及其绘制的基本规则；控制系统的根轨迹分析。

重点：概略绘制根轨迹的基本规则；根轨迹与系统性能的关系。

难点：开环零、极点分布与根轨迹形状间的对应关系。