2.2.2  传递函数与传递函数的零点和极点  

     1. 传递函数的定义与求法
    线性定常系统的传递函数定义为，在零初始条件下系统输出量的拉氏变换与输入量的拉氏变换之比。
    对于一般的线性定常单变量系统 ，设它由下列 n 阶常微分方程所描述 :

(2.22)
式中：y(t)为系统的输出量， u(t) 为系统的输入量，ai(i=0,1,···,n-1)和bj(j=0,1,···,n-1)是与系统的结构和参数有关的常系数。对上式取拉氏变换并令 Y(s)=L[y(t)] ，U(s)=L[U(t)]，经整理后可得
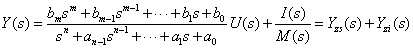(2.23)

    线性控制系统的传递函数具有下列特点：

    (1) 物理上可实现系统的传递函数通常为 s 的真有理函数

    (2) 控制系统的传递函数取决于系统的结构和参数，而与输入输出信号的形式无关

    传递函数与输入输出微分方程   当传递函数的分子与分母无公因子相消时，系统的传递函数与输入输出微分方程之间可以互相转换。

    传递函数的求法   求系统的传递函数有多种可供选择的方法：在工程上广泛采用结构图或信号流图法；也可直接根据传递函数的定义，或通过微分方程与传递函数之间的相互转换关系，由系统的微分方程求取传递函数；对于不同类型的系统也可采用专门的实用方法。

 
    有源校正装置传递函数的求法   求有源校正装置的传递函数或计算放大器的放大系数时通常采用“虚地”分析法。