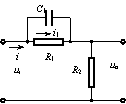
2.3.2   信号流图与梅森增益公式 

    图示线性系统的数学模型，除了应用结构图外还可采用信号流图。 它们都是通过图形既定性又定量地描述系统的结构，和信号的传递、变换以及各环节之间的控制关系。因此这两种图示方法是等效的，它们之间可以互相转化。

   信号流图的组成和常用术语   信号流图的基本组成单元有两个：节点和支路。 在图上节点用“○”表示，它代表系统的变量；各变量之间的因果关系用有向线段来表示，称为支路，支路的方向用箭头标明，信号只能沿着箭头单方向传递；两个变量之间的因果关系式叫做增益 ( 或传输特性 ) ，标在相应支路的旁边并叫做支路增益 ( 或支路传输 ) 。 支路起着乘法器的作用，支路增益就是环节的传递函数；图中每个节点所代表的变量值，等于该节点的各条输入支路的增益与相应的入端变量乘积之代数和。

    常用术语：   (动画:信号流图的相关术语)

    (1) 输入节点只有输出支路而没有输入支路的节点，称为输入节点或源节点。

    (2) 输出节点只有输入支路而没有输出支路的节点，称为输出节点或汇节点。

    (3) 通道沿箭头方向所连续经过的支路的集合叫做通道。 从输入节点到输出节点的开通道就是系统的前向通道，在前向通道上各支路增益的乘积称为前向通道增益。闭通道又叫做回路 ( 或回环 ) ，在回路中各支路增益的乘积称为回路增益。

    1. 信号流图的绘制    (动画:信号流图的绘制)   (动画:化结构图为信号流图)

    控制系统信号流图的绘制方法主要有两种： 一是根据微分方程来绘制；另一种方法是，根据信号流图与结构图之间的对应关系，由系统结构图转换而得。

    由系统的微分方程绘制信号流图任何线性方程都可用信号流图来表示。对于线性微分方程需先进行拉氏变换，将其转换为复变量 s 的代数方程组，然后再绘制系统的信号流图。 首先根据系统的工作原理确定系统的输入量、输出量和信号的传递流程以及流程中的各有关变量，并按照因果关系改写系统的代数方程组；然后用节点表示各变量，按照信号的传递关系从左往右排列，输入节点排在最左端，输出节点排在最右端；用支路表示信号的传递方向和相应的增益值；最后根据信号的传递关系，用支路将节点联接起来便可得系统的信号流图。如例图 2.30

图 2.30 RC 电路图

    2. 梅森增益公式    (动画:梅逊增益公式)

    应用梅森增益公式，它只需通过观察和简单的计算而不必进行繁琐的化简工作，则可求得系统中任意两个变量之间的传递函数。

    对于一般线性定常系统，信号流图上任意两个 ( 节点 ) 变量之间的增益 ( 即传递函数 )P ，可用下式计算：

                           (2.61)

式 (2.61) 称为梅森增益公式。 式中：Δ为信号流图的特征式，其值为

其中：① 为所有单独回路增益之和；②为所有互不接触回路中，每两个回路增益乘积之和；③为所有互不接触回路中，每r 个回路增益乘积之和，其符号由决定 (r=1，2，3，…) 。

    为输入节点至输出节点之间所有的前向通道增益，与其相应的余因子式乘积之和。其中Pk 为第 k 条前向通道的增益，Δk 为第k条前向通道的余因子式。

结构图改画成相应的信号流图。改画的基本思路是：

    (1) 根据信号流图与结构图的对应关系来改画   结构图的方块对应于信号流图的支路；环节的传递函数对应于信号流图的支路增益；结构图的信号线对应于信号流图的节点。

    (2) 精简节点数目使图形紧凑。