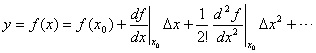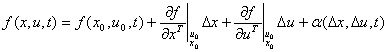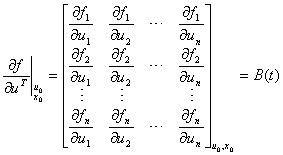2.4  实际控制系统数学模型的建立

        (动画:相似系统的微分方程)     

    (1) 准确性与实用性 建立控制系统数学模型的基本要求是，具有良好的准确性与简便性，并重在实用。

    (2) 线性模型与非线性模型 严格地说，一切实际系统都是非线性的。线性系统只是在忽略了次要的非线性因素后的一种理想化模型。
   

    2.4.1 非线性数学模型的线性化

    线性化的基本方法是：将非线性函数在平衡状态或参考轨迹附近展开成泰勒级数，只保留线性项从而将非线性模型线性化；而被忽略的泰勒级数的高阶项必须足够小，因此这种方法又称为小信号分析 ( 或小扰动 ) 理论。

    1. 非线性静态特性的线性化
    线性化的一般方法 设系统的输入输出特性

                                                                   (2.127)

将非线性方程 (2.127) 在工作点附近展开成泰勒级数：

忽略其高次幂项

                                        或                     (2.128)

写成线性模型的习惯表示形式：

                                                  Y=Kx

    2. 非线性微分方程的线性化
    非线性状态空间表达式的形式：

将非线性向量函数 f(x ， u ， t) 在参考状态轨迹附近展开成泰勒级数：

和

为非线性状态方程在参考轨迹处的雅可比 (Jacobi) 矩阵， 从而导出非线性控制系统 (2.129) 在参考轨迹附近的线性化状态方程为 

                                                    (2.131)