|
3.3 控制系统的零状态响应
基于输入输出模型系统的零状态响应 (动画:响应曲线与阻尼比的关系) 以符号 g(t) 表示系统的单位脉冲响应,为
系统零状态响应在复数域的表达式为
当 u(t)=δ(t) 时 U(s)=L[δ(t)]=1 ,于是在复数域系统的单位脉冲响应为 Y(s)=G(s) ,则 系统在任意输入信号作用下的零状态响应:在时域 可以表示为系统的单位脉冲响应与输入信号的卷积分 ( 如式 (3.15) 所示 ) ; 在复 ( 数 ) 域 可以表示为系统的传递函数与输入 ( 拉氏变换式 ) 的乘积 ( 如式 (3.16) 所示 ) ; 系统的单位脉冲响应与传递函数构成拉氏变换对 ( 如式 (3.17) 所示 ) 。 3.3.1 线性单变量系统的零状态响应 对于任意的输入信号 u(t) 均可分解成许多宽度为 △t 的窄脉冲之和。假设 u(t) 可分解成 N 个窄脉冲,于是任意形式的输入信号可用一系列的脉冲函数来逼近:
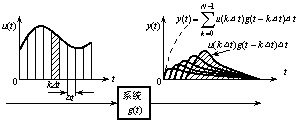
根据叠加原理,由任意输入信号 u(t) 作用于系统所产生的零状态响应,等于 u(t) 所分解成的各脉冲函数作用于系统所产生的零状态响应之和 ( 如图 3.1 所示 ) ,即
图 3.1 线性定常系统的零状态响应 当 △t→0 时上式的求和则可用积分来替换,近似相等就趋于准确相等。故可得线性单变量系统在任意输入信号作用下的零状态响应为
线性单变量系统零状态响应的零极点表示形式为
可见 线性单变量系统在任意输入信号作用下的零状态响应: 在时域可以表示为单位脉冲函数与输入的卷积分 ( 如式 (3.15) 所示 ) ; 在复数域 可以表示为传递函数与输入 ( 拉氏变换式 ) 的乘积 ( 如 (3.16) 所示 ) ,而由式 (3.18) 可见 系统的零状态响应特性取决于系统和输入信号的零极点分布; 而且 G(s) 与 g(t) 构成一拉氏变换对。 |
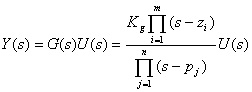 (3.18)
(3.18)