3.3.2 部分分式展开法
部分分式展开法的具体作法 在实际计算中,对于简单的象函数可直接查拉氏变换表便可求得其原函数;对于复杂的象函数 F(s) ,则可用部分分式展开法来求取原函数。即将 F(s) 展开成一些简单函数之和,设
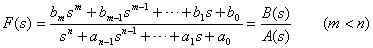
1. 只含互异极点的 F(s) 的部分分式展开
设 F(s) 的极点 pi (i=1 , 2 ,…, n) 为互异的单根,它们可以是实数或共轭复数。则 F(s) 可展开成下列部分分式之和:
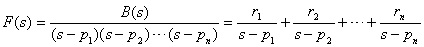
F(s) 的拉氏反变换为

共轭复极点成对处理 不妨设 F(s) 的极点为一对共轭复数,于是 F(s) 可展开为下列部分分式之和:
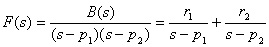
上式的拉氏反变换为
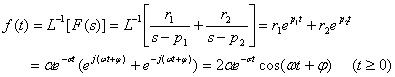 (3.19) (3.19)
2. 含有重根的 F(s) 的部分分式展开
方便起见,不妨设极点 p1 为 F(s) 的 m 重根,而其余的极点均为单根。于是 F(s) 可展开为下列部分分式之和:
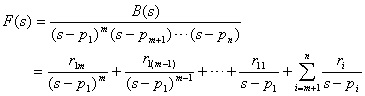 (3.20) (3.20)
上式的拉氏反变换为
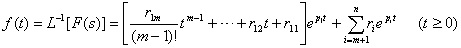
3. F(s) 为非严格真有理分式的部分分式展开
由于 部分分式展开法只适用于严格真有理分式函数 ( 即 m<n ) ,故当 F(s) 为非严格真有理分式 (即 m ≥ n) 时,需作预处理后才能进行部分分式展开。 将 F(s) 分解成一个商式 K(s) 和一个严格真有理分式 F'(s) 之和,即
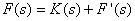
其中:商式 K(s) 为 s 的多项式,其拉氏反变换为单位脉冲函数 δ(t) 及其各阶导数的线性组合;而 F'(s) 为一严格真有理分式,可按上述部分分式展开法求其拉氏反变换。 |