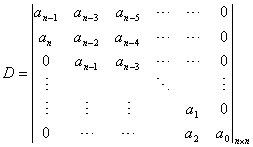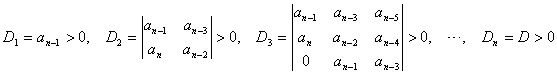| 3.4.3 劳斯- 赫尔维茨稳定判据
(动画:稳定判据) (动画:稳定判据应用) (动画:劳氏判据两特例) 线性定常系统的稳定性取决于系统极点的分布,故判断一个系统的稳定性便成为如何确定系统极点的分布问题。常用的方法有两类:一类是直接求解特征方程找出极点的分布情况;另一类是不必求解特征方程,而通过其它的简便方法就能确定极点的分布情况从而判断系统的稳定性。 1. 劳斯判据 线性定常系统的特征方程为
线性定常系统稳定的必要条件 线性定常系统稳定的必要条件是,特征方程的所有系数必须均为正的 ( 即系数同号 ) 。 线性定常系统稳定的充要条件 根据特征方程的系数构造下列阵列
其中
劳斯判据的结论如下: (1) 特征方程所有的根均具有负实部,即 线性定常系统稳定的充分必要条件为,劳斯表第一列的所有元素全为正的。 (2) 若劳斯表第一列的元素出现负的,则系统为不稳定的。而且分布在右半开平面上系统极点的个数,就等于第一列元素符号改变的次数。 (3) 若劳斯表的第一列出现“ 0 ” 元素,肯定系统不是稳定的。究竟是不稳定还是临界稳定的 ? 还需根据劳斯表作进一步判断。 (a) 如果阵列某行的第一列元素为零而其余各列的元素不全为零时 可以采用摄动的办法使“ 0 ” 元素不出现。 (b) 如果阵列某行的所有元素全为零时 它表明特征方程存在一些大小相等符号相反、关于原点对称的根。这时可用全零行的上一行元素作为系数组成—辅助多项式,然后用辅助多项式导数的系数代替全零行的各元素继续完成劳斯表的构造工作。 2. 劳斯判据的应用 (1) 分析参数变化对系统稳定性的影响,确定系统稳定时参数的取值范围 ( 即参数的稳定域 ) 。 (2) 确定系统的相对稳定性。 3. 赫尔维茨判据 赫尔维茨提出了另一种形式的代数判据。它以特征方程的各系数 ai( i =0 , 1 ,…, n) 构造 n × n 维的赫尔维茨行列式 D
线性定常系统稳定的充分必要条件为,赫尔维茨行列式的各阶主子式均大于零:
|
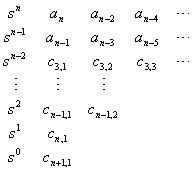
 (3.30)
(3.30)