从本节开始至第 6 章我们将系统地介绍一套工程实用的方法。其特点是: 以输入输出模型 ( 传递函数 ) 为基础 , 忽略零输入响应 ( 假定初始条件均为零 ) , 仅从零状态响应来考察系统的时间响应特性。它的前提条件是系统无零极相消 , 这符合绝大多数控制系统的特点。

    在这一节里将以低阶系统、主要是二阶系统的讨论为重点 , 并介绍高阶系统的工程分析方法。

    3.5.1   单位阶跃响应与性能指标       (动画:控制系统时域性能指标) 

    1. 典型输入信号与单位阶跃响应 目前广泛采用的确定性典型输入信号有下列五种: 单位脉冲信号 , 单位阶跃信号 , 单位斜坡 ( 或称单位速度 ) 信号 , 单位抛物线 ( 或称单位加速度 ) 信号以及正弦信号。

    典型响应 在上述四种典型输入信号 , 即单位脉冲、单位阶跃、单位斜坡和单位抛物线信号分别作用下系统的零状态响应

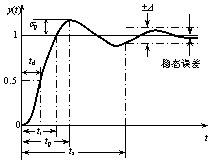
    相应地叫做系统的单位脉冲响应、单位阶跃响应、单位斜坡响应和单位抛物线响应。

    线性定常系统的一个重要特性 系统对输入信号导数的响应, 等于系统对该输入信号响应的导数 ; 系统对输入信号积分的响应 , 等于系统对该输入信号响应的积分。

    单位阶跃响应 通控制系统在零初始条件下由单位阶跃输入信号所产生的零状态响应, 简称为系统的单位阶跃响应。整个 ( 零状态 ) 响应过程可分解为两部分——暂态响应过程和稳态响应过程。所谓暂态响应过程是指 , 系统从初始状态到进入稳态之间的过渡过程。暂态响应过程结束后系统就进入稳态响应过程。相应地, 系统的 ( 零状态 ) 响应可分解为暂态响应与稳态响应两部分。

控制系统的典型单位阶跃响应曲线 , 如图 3.3 所示。

图 3.3 控制系统的典型单位阶跃响应曲线

    2. 性能指标

    与系统响应的两个分量 ( 暂态响应和稳态响应 ) 相对应地 , 性能指标也可分为两部分: 暂态性能指标和稳态性能指标。

    (1) 暂态性能指标：

    (a) 延迟时间td: 系统响应从 0 上升到稳态值的 50% 所需的时间。

    (b) 上升时间tr: 对于欠阻尼系统是指 , 系统响应从 0 上升到稳态值所需的时间 ; 对于过阻尼系统则指 , 响应从稳态值的 10% 上升到 90% 所需的时间。

    (c) 峰值时间tp: 系统响应到达第一个峰值所需的时间。

    (d) 最大超调量σp ( 简称超调量 ) : 系统在暂态过程中输出响应超过稳态值的最大偏离量。通常以单位阶跃响应稳态值的百分数来表示 , 即

    (e) 调节时间ts: 系统响应到达并不再越出稳态值的容许误差带±Δ所需的最短时间 , 即

    通常取Δ为稳态值的 5% 或 2% 。调节时间又叫做暂态过程时间或过渡过程时间。

    (f) 振荡次数N: 是指系统响应在调节时间 ts 的范围内围绕其稳态值振荡的次数。

    (2) 稳态性能指标通常用稳态时输出响应的实际值与希望值之差 , 即稳态误差来衡量系统的稳态控制精度或控制准确度。因此稳态误差就是控制系统的稳态性能指标。