3.5.2   一阶系统的暂态响应特性

    (动画:一阶系统的数学模型)  (动画:一阶系统的阶跃响应)

    一阶系统传递函数的一般表达式为

                    (3.33)

    微分方程为

    一阶系统的单位阶跃响应 由式 (3.33) 则可得一阶系统的单位阶跃响应为

                    (3.34)

或

                        (3.35)

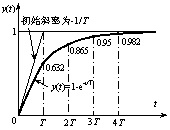
    相应的系统的单位阶跃响应曲线, 如图 3.4 所示。

 
图 3.4 单位阶跃响应曲线

可以看到 :

    (1) 一阶系统的极点为负实数, 相应的系统暂态响应为非周期响应

    响应曲线的变化率 由式 (3.35) 可得单位阶跃响应曲线的斜率为

    当 t =0 、 T 、 2T 和 3T 时 , 其斜率值分别为 、 、 和 。可见一阶系统暂态响应曲线的斜率也是单调变化的。

    (2) 一阶系统的暂态响应特性取决于时间常数 T ( 或系统极点 p )

当 t 分别等于 T 、 2 T 、 3T 和 4T 时 y(T) = 0.632 , y(2T) = 0.865 、 y(3T) = 0.95 和 y(4T) = 0.982 。

    一阶系统的暂态性能指标 根据暂态性能指标的定义

可求得一阶系统的延迟时间为

上升时间为

    当取 Δ 为不同值时则可求得一阶系统的调节时间为

                        (3.36)

系统的单位阶跃响应为非周期的, 超调量 σp 和峰值间 tp 均不存在。

    综上可见: 一阶系统的暂态响应特性取决于时间常数 T 的大小, 或系统极点 p 的分布 ( p = -1/T ), 而 T 又是反映系统的 T 惯性。因此一阶系统的惯性越小, 相应的时间常数也越小, 系统极点离虚轴便越远, 系统的响应就越快; 反之惯性越大, T 也越大, 系统极点离虚轴便越近, 系统的响应就越慢。

    一阶系统的单位脉冲响应 由式 (3.33) 可得一阶系统的单位脉冲响应为

或

                            (3.37)

该响应曲线的斜率为

当 t = 0、T、2T和∞时 , 其斜率值分别为 、 、 和 。

    可见: 一阶系统的单位脉冲响应是按指数规律单调变化的非周期响应; 响应曲线斜率的绝对值由初始时刻的最大值 , 随着时间的推移而不断减小直至趋于零;单位脉冲响应的特性也是取决于时间常数 T ( 或系统极点 p ) 的。

    对比一阶系统的单位阶跃响应曲线和单位脉冲响应曲线可以看到: 虽然两者的输入信号不同, 但是响应曲线的形状和变化规律则是相类似的, 它们所表征的系统特性也是一致的。