| 3.5.3 二阶规范系统的暂态响应特性
(动画:二阶系统动态性能指标) (动画:二阶系统动态性能的改善) 二阶系统传递函数的规范形式:
和
式中: ωn 称为 ( 闭环 ) 系统的无阻尼自然振荡角频率或自然频率 (rad/s);
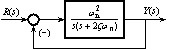
图 3.5 二阶规范系统结构图 # 二阶规范系统的单位阶跃响应 二阶规范系统的单位阶跃响应为
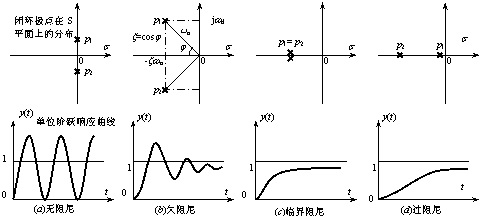
(1) 欠阻尼二阶规范系统的单位阶跃响应 这时 0<ζ<1 系统极点为一对共轭复根 :
可求得系统的单位阶跃响应为
(3.39) 或
可见 , 欠阻尼二阶规范系统的暂态响应特性取决于系统极点的分布。与一对共轭复极点相对应的系统暂态响应 , 为按指数规律衰减的简谐振荡 : 振荡的频率取决于极点的虚部 ωd; 而衰减的速度取决于极点的负实部ζωn 。 无阻尼二阶规范系统的单位阶跃响应 由式 (3.39) 或 (3.40) 令阻尼比 ζ =0, 则可求得无阻尼二阶规范系统的单位阶跃响应为
或
相应的单位阶跃响应曲线 , 如图 3.6(a) 所示。
无阻尼二阶规范系统的暂态响应特性也是取决于系统极点的分布。极点为虚轴上的一对共轭虚根, 相应的系统暂态响应为等幅振荡 , 振荡的频率等于极点的虚部 ωn 。 (2) 临界阻尼二阶规范系统的单位阶跃响应 这时 ζ=1 系统极点为一对负实重根:
由式 (3.38) 可求得系统的单位阶跃响应为
或
相应的单位阶跃响应曲线, 如图 3.6(c) 所示。 可以看到: 临界阻尼时系统的暂态响应特性, 同样也取决于系统极点的分布; 与一对负实重极点相对应的系统暂态响应, 为单调变化的非周期响应。 |
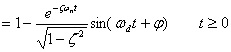 (3.40)
(3.40) 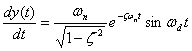 (3.41)
(3.41)