第4章  根轨迹法

4.1   根轨迹法的基本概念

    前已指出，系统的特性主要取决于闭环零极点的分布。闭环的零点易于确定，因而分析研究闭环系统特性的核心就在于，如何简便地、不需要求解特征方程的繁杂运算就能确定闭环极点的分布；另方面，闭环系统的性能往往可通过合理地选择系统的参数来达到，对于参数的变化如何简便地确定闭环极点的分布呢 ? 根轨迹法就是满足这些要求的一种工程实用方法。所谓根轨迹，就是当系统的参数变化时特征方程的根 ( 即闭环极点 ) 在 S 平面变化所描绘出来的轨迹。先考察小功率位置随动系统， 如图 4.2 所示。

 
图 4.2 小功率位置随动系统结构图

系统的特征方程为

于是特征方程的根 ( 即闭环极点 ) 为

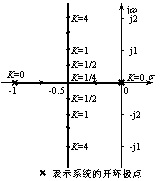
    当系统参数 K 在可能的取值范围 (0 ≤ K < ∞ ) 内变化时，特征方程的根在 S 平面上变化的轨迹，即系统的根轨迹为：当 K =0 时，两个闭环极点( p1 和 p2 ) 与两个开环极点 ( po1 和 po2 ) 相重合；当 K =1/4 时，两个闭环极点为实重根 ( 即 p1 = p2 =-1/2) ；当 0< K <1/4 变化时，闭环极点是在 -1 到 0 之间取值的两个相异的负实根；当 1/4< K <∞ 变化时，两个闭环极点为具有相同的负实部 (-1/2) ，而虚部随着 K 的提高而不断增大的共轭复根。于是可绘制闭环极点随着 K 变化的根轨迹曲线，如图 4.3 所示。

图 4.3 小功率位置随动系统的根轨迹图

    分析系统的根轨迹可以看到：

    (1) 系统的根轨迹曲线反映了系统特性的有关信息，可以根据根轨迹图对系统进行分析和设计：

    稳定性分析 由根轨迹图可见：无论开环增益 K 取何值，系统的根轨迹曲线和相应的系统极点均分布在 S 的左半平面上，故该闭环系统总是稳定的。

    暂态性能计算 当开环增益 K 为某一值时，由根轨迹曲线可确定闭环极点的具体位置，从而可求得系统的暂态性能。

    稳态特性分析 由根轨迹图上系统在坐标原点处的开环极点重数，则可决定系统的类型；由根轨迹上闭环极点的具体位置则可确定对应的开环增益 K ，从而可计算系统的稳态性能。

    参数设计 当可调参数 K 改变时，根轨迹曲线显示了闭环极点的变化情况及其趋势，于是可根据对系统性能的要求进行参数设计。

    (2) 根轨迹法的特点是：通过较简单的系统开环传递函数并利用图解的方法来分析或设计闭环控制系统；其基本思路与第三章所介绍的时域分析法是一致的。