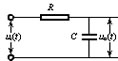
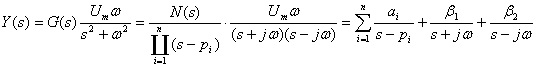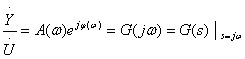第 5 章 频率响应法 频率响应法是控制理论的重要组成部分,是分析和综合控制系统的一种工程实用方法。它不仅适用于单变量系统,而且也可以推广至多变量系统。它的特点是:不必求解系统的高阶微分方程,可直接根据频率特性曲线的形状及其特征量来研究系统的性能。其突出的优点是:物理意义明确,可用实验的方法求出系统的频率特性和传递函数;而且计算量小,方法形象和直观,因而广为工程界所采用。根据它在系统分析和综合中的应用,将频率响应法分为两部分:频率响应分析法和频率响应综合法,并分别在第 5 章和第 6 章讨论。在这一章里主要介绍:频率响应法的基本概念和控制系统频率特性曲线的绘制方法,以及它在系统分析与综合中的应用,重点在于其基本概念和应用。 5.1 频率特性 (动画:频率特性) 频率响应法起源于通讯学科。它的基本思想是:将控制系统的变量也看作是信号;这些信号通过傅里叶 (Fourier) 分析,对于周期信号可展开为傅氏级数,对于非周期信号可进行傅氏变换,它们均可视为由不同频率成分的正弦信号所合成的;线性定常系统各个变量的运动,就是系统对各个不同频率信号响应叠加的结果。 频率响应法的优点:第一,这种方法具有鲜明的物理意义。第二,可以用实验方法测出系统的频率特性,并获得其传递函数以及其它形式的数学模型。第三,它是一种图解法,形象直观、计算量小。 频率响应法也存在一定的局限性:首先它只适用于线性定常系统。其次,频率响应法的筒便和实用性是以它的工程近似性为代价的。 5.1.1 频率特性的基本概念 (动画:频率响应的概念) 首先考察图 5.1 一阶 RC 电路图图 5.1 所示的简单系统。该系统为一阶 RC 电路。该电路的微分方程为 系统的传递函数为
图5.1 一阶RC电路图 若外施正弦输入电压
式中等号右边的第一项为输出响应的暂态分量,第二项为输出响应的稳态分量。当t趋于无穷大时第一项的暂态分量将趋于零,故系统的稳态输出响应为
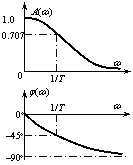
可以看到:在正弦输入电压作用下系统的稳态输出,是与输入同频率的正弦电压,其幅值为输入幅值的 它完全地描述了系统响应的特性。即在正弦输入电压作用下,稳态输出电压的幅值和相角的变化规律。它们是正弦输入电压频率的函数,故称函数1/(1+jωT)或G(jω )为该系统的频率特性函数 ( 简称频率特性 ) 。 相应地可绘制系统的频率特性曲线,如图 5.2 所示。
图5.2 一阶RC电路的频率特性曲线 线性定常系统的频率特性 对于一般的线性定常单变量系统, 系统的传递函数为
当输入信号为周期函数时 如果在输入端施加的为正弦信号
或
假设系统是稳定的,稳态响应分量
于是可定义线性定常系统的频率特性为,稳态时正弦输出信号的复数量与正弦输入信号的复数量之比,即
由上式可见,控制系统的频率特性等于其传递函数令s=jω置换的结果。频率特性的物理含义是:系统的幅频特性表示的是稳态时正弦输出信号与正弦输入信号的振幅之比;而相频特性表示的是正弦输出信号与正弦输入信号之间的相位差 。 当输入信号为非周期函数时 当输入与输出信号为非周期函数时,可以定义线性定常系统的频率特性为,输出信号的傅氏变换象函数与输入信号的傅氏变换象函数之比 。 结论: (1) 线性定常系统频率特性的定义 不论系统稳定与否,均将传递函数G(s)的s用jω置换的结果G(jω)称为系统的频率特性 。 (2) 频率特性与传递函数和输入输出微分方程一样都是系统的输入输出模型。 (3) 频率响应法是一种工程实用的图解法 不必求解系统的输出响应,而是根据频率特性曲线的形状及其特征量,就可确定系统的稳定性、暂态和稳态性能以及改善系统特性的基本途径 。
|
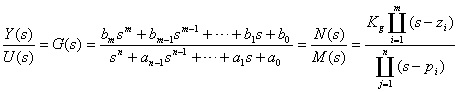 (5.4)
(5.4)