5.1.2   频率特性的图示方法

    1. 幅相频率特性图  (动画:相频特性曲线)

    以频率ω为参变量，绘制幅值与相位移关系的图形，就是系统的幅相频率特性图。

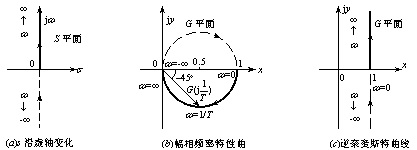
 图5.3 一阶系统的极坐标图

    线性定常集总参数系统的幅相频率特性曲线 (-∞<ω<∞) 是关于实轴对称的频率特性与逆频率特性之间的关系为：它们的幅频特性互为倒数；而相频特性差一负号 。即

                (5.7)

    2. 对数频率特性图 ( 又称伯德图 ) (动画:对数频率特性曲线)

    将系统的频率特性G(jω)=A(ω)ejφ(ω) 表示在对数坐标中，则可绘制对数幅频特性曲线和对数相频特性曲线，这样的图象叫做系统的对数频率特性图。故对数频率特性图又叫做伯德图。
    伯德图的特点   对数频率特性图是以 lgω为横坐标， 20lgA(ω) 或(ω) 为纵坐标的频率特性图。这就是说：系统的对数幅频特性是用

    作为纵坐标，线性分度，单位为分贝 (dB) ，如图 5.4(a) 所示， 对数相频特性的纵坐标为相位移 (ω) ，线性分度，单位为度 ( ° ) 或弧度 (rad) ；而它们的横坐标均为角频率ω，采用对数分度 ( 即按 lgω分度，但为了使用方便仍标以频率ω的值，其单位为 rad/s) 。ω与 lgω之间的对应关系，如表 5.1 所列。横坐标ω的对数分度与线性分度之间的区别，如 图 5.4(b) 所示。

  图5.4 伯德图坐标分度的特点

    采用伯德图的优点：

    (1) 能展宽视野。 由于横坐标采用对数分度后，ω变化10倍，横坐标( 即lgω) 只变化一个单位长度，即使ω变化 10000 倍，横坐标也只变化 4 个单位长度。因此在同一幅图上，可在很宽的频率范围内，把系统的低频、中频以及高频部分的频率特性均清晰地表示出来。
    (2) 运算方便。 控制系统的频率特性通常可表示为一些典型环节频率特性的相乘 (除) ， 采用伯德图后可化乘除运算为加减运算。
    (3) 绘制容易。 对数频率特性曲线的绘制，均有规律可循。
    (4) 简化频率特性与其逆的图形对应关系。互为逆的两个频率特性，其对数幅频特性和对数相频特性均分别互为反号；因而互为逆的对数幅频曲线和对数相频曲线都是关于横轴 ( 即零分贝轴或零度轴 ) 对称的。

    5.1.3  频率特性与零极点的关系

    系统频率特性的基本形状取决于系统零极点的分布。 频率特性以及相应的频率响应法，与前面介绍的时域法和根轨迹法具有内在的联系。