5.2.4 振荡环节与二阶微分环节的频率特性 (动画:典型环节的频率特性) 1. 振荡环节的频率特性 二阶振荡环节的传递函数为
幅相频率特性 由式 (5.11) 可得振荡环节的频率特性为
其中
分析式 (5.12) 可以看到:当ω=0 时,A(0)=1 ,φ(0)=0°;当ω→∞时,A(∞)=0 ,φ(∞)=-180°;当ω=ωn时,A(ωn)=1/(2ζ) ,φ(ωn)=-90°。 对数幅频特性 由式 (5.12) 可得,振荡环节的对数幅频特性为
当ω<<ωn时,式 (5.13) 可近似表示为
当ω>>ωn时,式 (5.13) 可近似表示为
这表明振荡环节的高频渐近线,是一条斜率为 -40dB/dec的直线。当ω=ωn= |p1| = |p2| 时两条渐近线相交。于是 称相交点频率ωn为振荡环节的交接频率或转折频率,其值等于该环节复极点的模。 渐近曲线所造成的误差主要发生在转折频率的附近。其误差为:在低频段 (0<ω<ωn)
在高频段 (ωn<ω<∞)
根据以上关系式则可绘制振荡环节对数幅频特性的误差修正曲线。若对渐近幅频曲线的误差加以修正,则可得振荡环节的准确对数幅频曲线。 谐振频率ωr与谐振峰值 Mr由对数幅频曲线可以看到,当ζ比较小时在ω=ωn的附近将出现谐振峰值。这说明:振荡环节对于输入信号中频率接近ωn的那些谐波分量的增益特别大,因而在输出信号中这些谐波分量的影响将突出地表现出来。谐振点是幅频曲线的驻点, 解得谐振频率为
求得谐振峰值为
可以看到:当0≤ζ≤0.707时振荡环节的谐振峰值 Mr是阻尼比ζ的单值函数,它随着ζ的减小而不断地增大,当ζ→0 时 Mr→∞;而 谐振频率ωr低于无阻尼自然振荡频率ωn和阻尼振荡频率ωd( 对数相频特性 由式 (5.12) 可得,振荡环节的相频特性为
当ω=0 时φ(0)=0°;当ω=ωn时φ(ωn)=-90°;当ω=∞时φ(∞)=-180°。 2. 二阶微分环节的频率特性 二阶微分环节的传递函数和频率特性分别为
二阶微分环节的传递函数是振荡环节传递函数的倒数。因此二阶微分环节的极坐标图是振荡环节的逆极坐标图;其对数幅频特性和对数相频特性与振荡环节的只差一个负号,于是二阶微分环节的对数频率特性曲线与振荡环节的对数频率特性曲线是关于ω轴对称的。 |
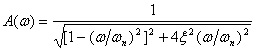
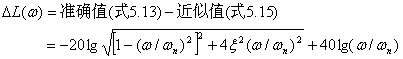
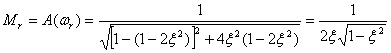 (5.17)
(5.17)