| 5.3 控制系统频率特性图的绘制
频率响应法的一个突出特点是：利用易于绘制的系统的开环频率特性曲线，来分析或综合闭环控制系统。因此绘制系统的频率特性图，主要在于绘制系统的开环频率特性曲线。
(动画:最小相位系统的频率特性) 通常闭环系统的开环传递函数和开环系统的传递函数以及较简单反馈系统的闭环传递函数，易于写成式 (5.20) 所示的规范形式。 系统的频率特性可以表示为
其中
上式表明：控制系统的幅频特性等于各组成环节幅频特性相乘；系统的相频特性等于各组成环节相频特性相加。 5.3.1 控制系统伯德图的绘制 (动画:典型伯德图绘制举例) 由式 (5.21) 可得，控制系统的对数频率特性为
上式表明： 控制系统的对数幅频特性和对数相频特性，等于各组成环节的对数幅频特性和对数相频特性分 d 别相加。 由式 (5.20) 可得，当ω趋于零时系统的频率特性为
故控制系统对数频率特性的低频渐近线为
式 (5.22) 表明： 对数幅频曲线的低频渐近线为一直线，其斜率为 -20ν dB/dec，即斜率的大小取决于串联积分环节的阶数ν；渐近线的位置取决于增益K，由式 ( 5.22a ) 可得渐近线 ( 或其延长线 ) 与ω=1 垂直线的交点所对应的幅值为 20lgK；而 对数相频曲线的低频渐近线也是一直线，其相角为 - ν×90°。 绘制伯德图的一般步骤 工程上常用更简便的方法来绘制系统的对数幅频曲线。 其基本思路是： 为了快捷地对系统进行初步分析或综合，在实际工作中往往只需要绘制系统的对数渐近幅频曲线；而各典型环节，除了比例、积分和微分环节外，其对数渐近幅频曲线的低频渐近线均为零分贝线，故各环节对数渐近幅频曲线相加，实际上只需对转折频率后的高频段进行；转折频率在数值上等于零极点的模；如果需要绘制准确的幅频曲线，只需对渐近幅频曲线进行误差修正。因此绘制系统伯德图的一般步骤可归纳如下。 1. 对数幅频曲线 (1) 将传递函数改写成式 (5.20) 所示的规范形式。 (2) 绘制对数幅频曲线的低频渐近线。在图上确定ω=1 和L(ω)=20lgK的点，由该点往左画斜率为 -20νdB/dec的直线，其中ν为积分环节的阶数。该直线便是对数幅频曲线的低频渐近线。 (3) 绘制对数渐近幅频曲线首先根据传递函数零极点的模，确定渐近幅频曲线的转折频率，并将它们由小到大依次标在ω轴上；然后由上述的低频渐近线开始，沿频率增大的方向自左往右逐段绘制渐近曲线。遇到转折频率处曲线就转折，渐近曲线的斜率便发生变化：每经过一个实数极点 ( 或实数零点 ) 所对应的转折频率后，渐近曲线的斜率就变化 -20dB/dec( 或 +20dB/dec) ；每经过一对共轭复数极点 ( 或共轭复数零点 ) 所对应的转折频率后，渐近曲线的斜率就变化 -40dB/dec( 或 +40dB/dec) ；当所有的转角频率都通过后，就完成了对数渐近幅频曲线的绘制工作。 (4) 如果需要，对转折频率附近的渐近曲线进行修正，便可得准确的对数幅频曲线。 2. 对数相频曲线的绘制 画出各组成环节的对数相频曲线，然后逐点将它们相加则可绘制系统的对数相频曲线。 对数相频概略曲线的绘制 在工程上往往并不需要准确地画出系统的对数相频曲线，而只要求能快捷地勾画出它的大致形状。这时不必将每个环节的相频曲线都画出来再逐点相加，而可直接 根据若干重要频率点的相角值和各组成环节相频特性的特点以及相频曲线的变化范围，便可概略地绘制系统的对数相频曲线。 |
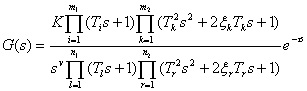(5.20)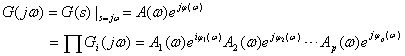 
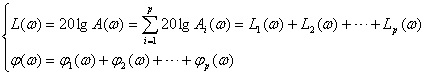
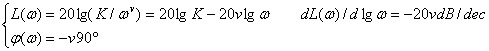(5.21) 
(5.22)