| 5.3.2 控制系统极坐标图的绘制 (动画:幅相曲线绘制举例)
控制系统频率特性G(jω) 的极坐标图,是当ω从 0 变化至∞时表示在极坐标上G(jω) 的幅值与相角的关系图象。其常用绘制方法有三种:直接计算法、伯德图法和应用 MATLAB 等计算机软件来绘制。其中伯德图法,是利用对数频率特性易于绘制的优点,先画系统的伯德图并从图上获得在不同ω下的幅值和相角数据,然后利用这些数据则可绘制系统的极坐标图。 直接计算法 其做法是:在ω的取值范围内,给定一系列ω值分别计算对应的幅值和相角,根据这些数据则可绘制系统的极坐标图。现举例说明如下。 最小相位系统幅相频率特性曲线的一般形状 大多数控制系统的零极点均分布在 S 的左半闭平面上,其传递函数的一般表示形式
式中n≥m。对于这一类常见的最小相位系统,其幅相曲线的一般形状具有下列特点: (1) 低频部分 由式(5.23) 可得,频率特性的起始部分为
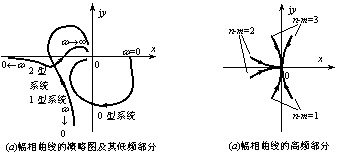
上式表明, 幅相曲线的低频部分取决于系统类型ν和增益K。各型系统幅相曲线低频部分的一般形状,如图5.9(a) 所示。 (2) 高频部分 由式(5.23) 可得,频率特性高频部分的幅值和相角分别为
这表明: 当ω趋于∞时幅相曲线收敛于坐标原点 ( 当n>m时 ),或实轴上某一有限值点 ( 当n=m时 );而曲线的方向由式(5.38) 决定。 如图5.9(b) 所示。 (3) 中间部分 分析式(5.23) 可得 幅相曲线中间部分的复杂形状是由零极点的复杂分布所造成的。 根据以上特点,不难绘制各种类型最小相位系统的概略幅相频率特性曲线。
图5.9 各型最小相位系统的极坐标图 |
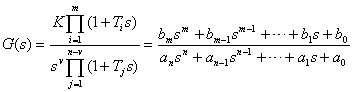 (5.23)
(5.23)