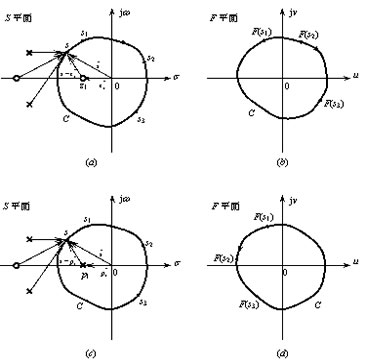
稳定性判别方法，是利用系统的开环频率特性来判断闭环系统的稳定性。它由奈奎斯特 (H.Nyquist) 于 1932 年首先提出的，故命名为奈奎斯特判据，简称奈氏判据。

    奈奎斯特稳定判据是从闭环系统的特征方程 1+Gk(s)=0 ( 如式 (5.26) 所示 ) 出发，并建立在复变函数的映射定理的基础之上的。

    5.4.1  映射定理   (动画:奈奎斯特围线)

    一个复变函数F(s) 可视为从复数域到复数域的映射。如果复数s=σ+jω用S平面来表示，复变函数F(s) 用复平面 ( 简称F平面 ) 上的图形来表示，则F(s) 就是从S平面到F平面的映射。如图5.12 所示。

图5.12 映射定理的示意图

    如果在S平面上的某一封闭曲线C内包含有F(s)的P个极点和Z个零点且该闭曲线不通过F(s)的任一零点或极点，当s沿闭曲线C顺时针方向连续变化一周时，则F(s) 对应的闭曲线C′沿逆时针方向包围坐标原点的周数 N 为

N=P–Z                                  (5.29)

    这就是映射定理。当F(s)含有时滞环节时，可以证明上述定理仍然成立。