5.4.2   奈奎斯特稳定判据   (动画:开环系统含积分环节的奈奎斯特围线)

    取闭曲线 C 为包围整个右半 S 平面并沿顺时针方向变化的封闭曲线，如图5.13 所示。

图5.13 S平面的D形围线

将F(s) 与闭环系统的特征多项式联系起来，令F(s)=1+Gk(s) ，其中系统的开环传递函数的基本形式如式 (4.7) 所示，即

                (5.30)

于是

                (5.31)

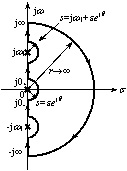
    上式表明：这时F(s) 的分母为开环传递函数的分母多项式；F(s) 的分子为闭环系统的特征多项式。于是映射定理 ( 式 (5.29)) 应用到这种情况其具体含义是：F(s) 在右半开平面内的极点数P，就是分布在右半开平面内的开环极点数；F(s) 在右半开平面内的零点数Z，就是分布在右半开平面内的系统极点数。而由 3.4.1 小节可知：要使闭环系统稳定，系统极点必须均分布在S的左半开平面上，或者说不能有系统极点落在右半开平面内，即Z=0 。这样由映射定理便可导出反馈控制系统的稳定性判据。

    1. 奈奎斯特稳定判据

说明如下：

    (1) 函数 1+Gk(s) 的图象包围坐标原点的周数，等于Gk(s) 的图象包围 (-1，j0) 点的周数。

    (2) 可用开环频率特性曲线Gk(jω) 取代Gk(s) 的图象， 来判断闭环系统的稳定性。

    (3) 若有系统极点分布在虚轴上，则Gk(jω) 曲线将穿过 (-1，j0) 点。

    (4) 若有开环极点分布在虚轴上，则应采用广义D形围线。如图5.14 所示。 这时位于虚轴上的开环极点 ( 包括位于原点上的开环极点 ) 均作为分布在左半平面上看待。

图5.14　S平面的广义D形围线

    这样由映射定理 ( 式(5.29)) ，则可导出奈奎斯特稳定判据如下：

    (1) 若 Z=0 由式(5.29) 可得N =P。这就是说： 如果系统在右半开S平面上有P个开环极点时，则闭环系统稳定的充要条件为，当ω从 -∞变化至 + ∞时开环频率特性曲线Gk(jω)逆时针方向包围临界点 (-1，j0)P周。

    (2) 若N≠P 由式(5.29) 可得Z =P-N。这就是说： 如果Gk(jω) 曲线 (-∞<ω<∞) 包围临界点的周数N不等于系统在右半开平面上的开环极点数P，则闭环系统不稳定，而且分布在右半开平面上的系统极点个数为Z =P-N。

    (3) 若闭环系统临界稳定，则Gk(jω) 曲线将穿过临界点。

    应用奈氏判据确定闭环系统稳定性的实用方法 由于Gk(jω) 与Gk(-jω)(0≤ω<∞ ) 是复共轭的，它们的图形是关于实轴对称的。因此实际应用时可以加以简化：只绘制 0≤ω<∞的开环频率特性曲线G(jω)，并根据它对临界点 (-1，j0) 的包围周数Nh来判断闭环系统的稳定性。 由于 0≤ω<∞的G(jω) 曲线对临界点的包围周数Nh，只有 - ∞<ω<∞开环频率特性曲线对临界点包围周数N的一半。因此，只要令N =2Nh，并将映射定理 ( 式(5.29)) 改写成下列形式

Z =P–2Nh                        (5.32)

    如果系统的开环传递函数含有ν个积分环节，则在绘制ω从 0+ 变化至∞的开环频率特性曲线Gk(jω)后，应从Gk(j0+) 点开始沿逆时针方向补画半径为无穷大、绕过ν×90 °的圆弧。