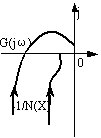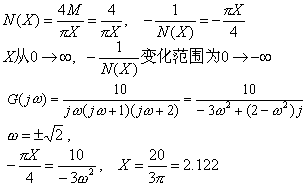7.4　用描述函数法分析非线性系统

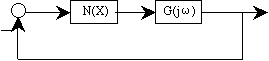
　　假设非线性元件和系统满足应用描述函数法的条件，则非线性部分可以用描述函数N(X)表示，线性部分可以用传递函数和频率特性表示。
　　于是，非线性系统可以看看成一个等效的线性系统，并应用线性理论中的频率判据来判定闭环系统的稳定性。
　  7.4.1 用描述函数法分析非线性系统的稳定性  (动画:非线性系统的稳定性)
　　1．非线性系统的稳定性
　　所谓非线性系统是稳定的，即非线性系统受到扰动以后，能够恢复到原来的平衡位置附近；若非线性系统受到扰动后，其输出增大，不能恢复到原来的平衡位置附近，该非线性就是不稳定的。
　　2．用描述函数法分析非线性系统的稳定性
　　在非线性系统中，在只考虑基波的情况下，将线性理论中的乃奎斯特稳定判据推广应用于非线性系统，由图7.5所示。

 　　 　　　　　　　　　　　图7.5　　　　　　　

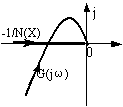
 　  类似的闭环特征方程为：

　　　　 被称为负倒描述函数。

　　非线性系统存在自激振荡的必要条件：非线性系统部分的负倒相幅相特性与线性部分的频率特性相交。

　　判断非线性系统的稳定性判据：

　　设非线性系统的线性部 具有 最小相位性质 。

　　1）若 曲线包围 曲线，则非线性系统不稳定；

　　2）若 曲线不包围 曲线，则非线性稳定；

　　3）若 曲线和 曲线相交，则系统存在周期运动；若当振幅X增大时， 曲线由 包围的区域（不稳定区）穿出，该交点处存在着稳定的周期运动，该交点是自振点。

　　实际应用中可以 曲线与 曲线的相对位置来判断非线性系统的稳定性，也可以用 曲线与 曲线的相对位置来判断非线性系统的稳定性。 称作非线性系统的尺度系数。描述函数是相对描述函数 与尺度系数 之积，即

　　3．判别非线性系统稳定性的步骤

　　第一步：绘制非线性部分的负倒幅特性。

　　求非线性部分的负倒描述函数 ，并作出相对负倒描述函数曲线 。

　　第二步：作线性部分的幅相频率特性 。

　　列表计算 值，将相对负倒描述函数曲线 与 同作在一张图上。

　　第三步：判别非线性系统的稳定性。根据 曲线与 曲线的相对位置判别系统的稳定性。

　  7.6.2 用描述函数法分析自激振荡  (动画:非线性系统的周期运动分析)

　　自激振荡，是一种振幅能自动恢复的周期运动，是一种稳定的周期运动。

　　在非线性系统中，如果存在 = 或 = ，则系统处于等幅振荡状态，是周期运动状态。处于周期运动状态的不一定是自振。只有稳定的周期运动才称之为自振。换言之，自振点都在 与 的交点上，但是 与 的交点不都是自振点。

　　判断交点是否为自振点的方法：若当振幅 X增大时， -1/N(X)曲线由G(jω)包围的区域（不稳定区）穿出，该交点处存在着稳定的周期运动，该交点是自振点。

　　确定非线性系统自振点及自振参数步骤为：

　　第一步：根据非线性特性查表或求出 。

　　第二步：计算 及 ，在同一张图上作出 及 曲线。

　　第三步：确定自振点。由 包围的区为不稳定区。 曲线由不稳定区穿出到稳定区的 与 的交点为自振点。

　　第四步：确定自振参数 、 。自振点是 与 的交点，此交点处 曲线对应的 为该自振点的频率；此交点处的 对应的 值为该自振点的振幅 。

    例7.3 非线性系统的 G(jω)曲线和-1/N(X)曲线如图7.6所示，试判断各闭环系统是否稳定及是否有自振。

　　解：
　　a）图中，G(jω)曲线和-1/N(X)曲线存在交点，即存在周期运动。当振幅X增大时， -1/N(X)曲线由G(jω)的稳定区穿出，所以不是自振点。系统不存在自振。
　　b) 图中，G(jω)曲线和-1/N(X)曲线存在交点，即存在周期运动。当振幅X增大时， -1/N(X)曲线由G(jω)包围的区域（不稳定区）穿出，所以是自振点。系统存在自振。

 　 c) 图中，G(jω)曲线和-1/N(X)曲线无交点，所以不存在周期运动。可以看出， 曲线包围了 曲线，所以非线性系统不稳定。

　　例7.4  用描述函数法分析下面非线性系统是否存在自振？若存在，求振荡频率和振幅。

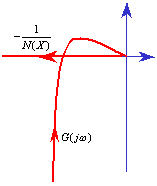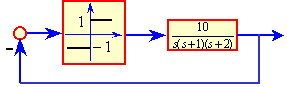 　 解：  

 　　。

　　 7.4.3　利用非线性改善系统性能
　　 在系统中适当地引入非线性特性，可以改善系统性能。