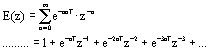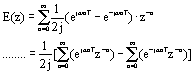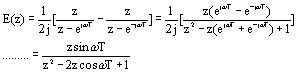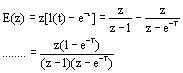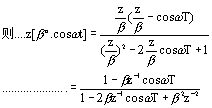8.2 Z 变换与 Z 反变换 (动画:z变换) |
||
8.2.1 Z变换 |
||
由采样过程的数学描述知，离散信号的拉氏变换为  ，令 z=eTs ，则  =e(0)+e(T)z-1 +e(2T)z-2 +… 即为 Z 变换的定义式。 称 E(z) 为离散信号 e*(t) 的 Z 变换，记作 Z[e*(t)]=E(z) ，或 Z[e(t)]=E(z) |
||
| 2. Z变换方法 (1) 级数求和法 将Z变换的定义式展开： E(z)=e(0)+e(T)z-1+ e(2T)z-2+…+ e(nT)z-n+…对于常用函数Z变换的级数形式，都可以写出其闭合形式。 (2) 部分分式法 ① 先求出已知连续时间函数e(t)的拉氏变换E(s)； ② 将E(s)展开成部分分式之和的形式； ③ 求拉氏反变换，再求Z变换E(z)。 |
||
| 3. 典型信号的Z变换
(1) 单位脉冲函数 e(t)= δ(t) (2) 单位阶跃函数 e(t)=1(t) (3) 单位理想脉冲序列 e(t)=δT(t) (4) 单位斜坡信号 e(t)=t ，则 对比（2）中结果，有 两端对 z 求导数，得 两边同乘 (-Tz) ，得单位斜坡信号的 z 变换 (5) 指数函数 e(t)=e-aT (a 为实常数 ) 这是一个公比为 (e-aTz-1 ) 的等比级数，当 |e-aTz-1|<1 时，级数收敛，则可写成闭合形式 (6) 正弦信号 e(t)=sinωt 因为 利用(5) 中结果，有; 例8.1 解：先进行部分分式展开，有 再取拉氏反变换 参照 (2) 和 (5), 得： 4. Z变换的性质 (1) 线性定理 若 E1(z)=Z[e1(t)] ， E2(z)=Z[e2(t)] ， a 为常数，则 Z[e1(t)+e2(t)]= E1(z)+ E2(z) ， Z[ae(t)]=aE(z) 。 (2) 实数位移定理 若 E(z)=Z[e(t)] ，则 Z[e(t-kT)]=z-kE(z), Z[e(t+kT)]= 例8.2 已知 e(t)=1(t-T), 求 Z 变换 E(z) 。 解： (3) 复数位移定理 已知 e (t) 的 z 变换为 E(z) ，则有 例8.3 已知 e(t)=te-at , 求 Z 变换 E(z) 。 解： 已知单位斜坡信号的 z 变换为 根据复数位移定理，有 (4) z 域微分定理 (5) z 域尺度定理 例8.4 试求 bncosωt 的 Z 变换。 解： 由 z 变换表 (6) 初值定理 (7) 终值定理 (8) 卷积定理 设 x(nT) 和 y(nT) 为两个采样函数，其离散卷积定义为 x(nT)*y(nT)= 8.2.2 Z 反变换 从 Z 域函数 E(z) 求时域函数 e*(t) ，叫做 Z 反变换。记作 Z-1[E(z)]= e*(t) 。 1. 部分分式展开法 部分分式展开法是将 E(z) 展成若干分式和的形式，对每部分分式查 Z 变换表找出相应的 e*(t) 。因 Z 变换表中 Z 变换函数分子普遍有因子 Z ，所以应将 E(z)/z 展开成部分分式。 例8.5 已知 z 变换函数 解： 首先将 E(z)/z 展开成部分分式 所以 e(nT)=(-1+2nT) 10 e * (t)=e(0)d(t)+e(T)d(t-T)+e(2T)d(t-2T)+… =0+10d(t-T)+30d(t-2T)+ 70d(t-3T)+… 例8.6 已知 z 变换函数 解： 因为 查 z 变换表 , 得 e(t)=1(t)-e-at 则 e(nT)=1-e-anT 所以 e*(t)=e(0) d(t)+e(T)d(t-T)+e(2T)d(t-2T)+… =0+(1-e-aT )d(t-T)+(1-e-2aT )d(t-2T)+(1-e-3aT )d(t-3T)+… 2. 幂级数法（综合除法） 由 Z 变换的定义 而  。 |
||
，所以：
。 
。 
。 
， 
。 
。 
存在，则 
。 
存在，则 
。 
，则卷积定理为： Z[x(nT)*y(nT)]=X(z)Y(z) 。 
试求其 z 反变换。 
，
